After Lewis had completed his Missouri Headwaters observations, the celestial data would need to interpreted to determine their location.
Celestial Observations at the Three Forks of the Missouri 28-29 July 1805.
Missouri River Headwaters
View from Fort Rock (north)
© 23 July 2013 by Kristopher K. Townsend. Permission to use granted under the Creative Commons Attribution-Share Alike 4.0 International license.
On 15 July 1805, after having spent a month in the area near the Great Falls of the Missouri, the canoes that had been portaged around the falls and the new ones built at Canoe Camp, finally headed upstream; they were laden to the gunnels. The next day the explorers passed a meander bend bristling with about forty willow lodges; an experienced eye determined that these lodges had been abandoned only 10 to 12 days earlier. Inasmuch as this willow-lodge camp was only about 12 miles on a direct line southwest of the expedition’s White Bear Islands Camp it is possible that the people who camped here had observed the activities of the expedition at that camp or had seen its hunters. The captains concluded that these lodges had been built and occupied by Shoshones, but this is not necessarily so.
As the expedition continued upstream, the captains daily expected to meet the Shoshone. They found well-traveled trails, more abandoned lodges, even a smooth-bore trade musket, but no Shoshone. Perhaps the firing of the hunters’ guns induced the cautious Shoshone to keep out of sight. The captains held council: If a small scouting party was sent ahead on foot it might be able to make contact with these people whose horses certainly would be needed when the expedition crossed to the Columbian waters.
Clark drew the assignment, and after the expedition passed the mouth of Dearborn River on 18 July 1805, he set out on foot with a few men to seek the Shoshone. Clark’s party saw a horse and found a bow. They also found a multitude of prickly pear cactus spines, but no Shoshone.
Arrivals
Seven days later, on 25 July 1805, Clark and his party reached the Three Forks of the Missouri. Although the south fork (Madison) and the west fork (Jefferson) were essentially the same size, Clark—even before examining these rivers upstream—left a note for Lewis recommending the west fork. Not surprising. . . . Clark had had enough of traveling south; it was time to head west!
Meanders more than doubled the distance that the canoe party had to struggle upstream compared to Clark’s overland route. Nevertheless, on the morning of 27 July 1805, just two days behind Clark, the canoe party, after traveling several miles through a narrow canyon, reached a valley that opened wide before them. Lewis, with no less geographic instinct than Clark, knew that he had arrived at the Three Forks of the Missouri. He halted the canoes opposite the mouth of the east fork (Gallatin) and, while most of the others began to eat their breakfast, he had himself ferried across to the east side of the river. He then hiked up along the east fork until he found a place where he could ascend a limestone promontory. From that vantage point he studied the country ahead and sketched the meanderings of the rivers. After he returned to the canoe party they all continued a short distance upstream to the junction of the Madison and the Jefferson. There Lewis found Clark’s note and, following Clark’s advice, directed the canoes up the Jefferson. About a mile farther up this river, on a wedge of land between it and the Madison, Lewis made camp, calling this island Camp Island. The expedition’s camp here, commonly called Three Forks Camp, was at or near 45°55’44” N, 111°30’40” W as determined from the expedition’s river survey, early and modern maps and from aerial photos.
About noon Clark rejoined the canoe party at this camp and gave Lewis an overview of the geography along both the southwest and west fork as far as he had scouted. That evening Lewis wrote: “beleiving this to be an essential point in the geography of this western part of the Continent I determined to remain at all events untill I obtained the necessary data for fixing it’s latitude Longitude &c.”
Schedule of Observations
On 28 July 1805, while a fever-ridden Clark drew maps, Lewis began his celestial observations. By late night on 29 July 1805, Lewis had completed ten discrete celestial observations consisting of a total of forty-eight separate angular measurements. Two of these were for the sun’s noon altitude; eleven were to check his chronometer, thirty were for longitude and five for magnetic declination.
The only calculations that Lewis made from the celestial observations he took at Three Forks Camp were for latitude, and he made these using an index error for his octant of 2°40′; it should have been 2°11’40”. While at Fort Clatsop Lewis discovered that he had used the wrong index error for the octant during 1805 and recalculated some of the latitudes. The latitude of the Three Forks, however, was not among them.
Suppose, however, that Lewis had recalculated the latitude of the Three Forks Camp using the correct index error; and suppose further that Lewis, while at Fort Clatsop, had determined the chronometer’s error on Local Time and its daily rate of loss from his Three Forks observations. He then could have calculated the longitude and magnetic declination from the observations he made there. What longitude and magnetic declination might those calculations have yielded if Lewis had used 111° W for his “dead-reckoned” longitude (the Three Forks are shown at about 110°50′ W on the Lewis and Clark map of 1806; Moulton, Atlas, map 123).
At 111° W the time difference from Greenwich would be 7 hours and 24 minutes. Thus, for example, when Lewis made his meridian observation of the sun at Local Noon, the Greenwich Apparent Time would have been 19:24:00 or 7:24 p.m.
The following are the separate observations that the captains made at their camp near the Three Forks; all data are from Lewis:
| Date | Type of Observation | Number of Measurements and Description |
|---|---|---|
| 28 | Equal altitudes of the Sun AM | 3, altitude of the sun + the time |
| 28 | Meridian (noon) altitude of the Sun | 1, sun’s altitude at its highest daily point in the sky |
| 28 | Equal altitudes of the Sun PM | 2, altitude of the sun + the time (clouds blocked no. 3) |
| 29 | Magnetic declination of the Sun | 2, sun’s altitude and bearing + the time |
| 29 | Equal altitudes of the Sun AM | 3, altitude of the sun + the time |
| 29 | Meridian (noon) altitude of the Sun | 1, sun’s altitude at its highest daily point in the sky |
| 29 | Equal altitudes of the Sun PM | 3, altitude of the sun + the time |
| 29 | Lunar distance from the Sun 1 | 10, angle between the moon and sun + the time |
| 29 | Lunar distance from the Sun 2 | 10, angle between the moom and sun + the time |
| 29 | Magnetic declination of the Sun | 2, sun’s altitude and bearing + the time |
| 29 | Lunar distance from Antares | 10, angle between the moon and Antares + the time |
| 29 | Magnetic declination of Polaris | 1, bearing of Polaris + the time |
Latitude
While at camp on Camp Island near the Three Forks of the Missouri, Meriwether Lewis took two observations of the sun’s noon (meridian) altitude for latitude. He calculated latitudes from these observations and, from them, obtained an average of 45°24’08.5″ N. Lewis’s average, unfortunately, lies more than 36 miles south of the camp’s redetermined latitude of 45°55’44” N (see Table I). The principal reason for this difference stems from Lewis’s use of the wrong index error for his octant.
If Lewis had used an index error of 2°11’40.3″[1]This is the value Lewis recorded in 1804 in his journal entry for 22 July 1804 (see Moulton, Journals 2:411) and again in the Fort Clatsop Miscellany (Ibid., 6:496). Even though Lewis left no … Continue reading
90° |
Zenith [this calculation can be omitted] |
– 45°23'23" |
latitude that Lewis derived |
44°36'37" |
co-latitude, |
+ 18°45'36.7" |
declination (Lewis may have used a slightly different value) |
63°22'13.7" |
true altitude of sun’s center |
– 00°15'47.2" |
sun’s semidiameter |
– 00°00'04" |
parallax |
+ 00°00' 24.5" |
refraction |
63°06'47.0" |
apparent altitude |
x 2 |
|
126°13'34.0" |
double altitude because of artificial horizon |
180° |
|
53°47'26" |
observed angle + index error |
59°07' |
observed angle |
+ 5°20'34" |
octant’s index error |
÷ 2 |
|
+ 2°40'17" |
after rounding = +2°40′ = half index error (correction = -2°40′). This value of 2°40′ is the (half) octant error that Lewis recorded on 12 April 1804 at the mouth of the Little Missouri River and incorrectly used throughout 1805 except at Fortunate Camp. |
Instead of 2°40′ and an estimated longitude of 111° W when he calculated the latitudes from these observations he should have derived an average latitude for this camp of 45°51’02” N. This latitude, however, still is about 4’42” (5½ miles) too far south of the redetermined latitude for the expedition’s camp on Camp Island.
This difference in latitude could have resulted from observational errors that Lewis made, but it is much more likely that the octant, though made of seasoned wood, had warped slightly from the low humidity that is so common to southwestern Montana summers, thereby changing the octant’s index error. Lewis should have checked the index error of both octant and sextant regularly because handling, transporting, humidity and temperature can affect the index error of these sensitive instruments.
| Date | Lewis, 1805 | Recalculated (This study) |
Redetermined latitude (map evaluation) |
|---|---|---|---|
| 28 July 1805 | 45°24’54” north | 45°50′ 04″ north | |
| 29 July 1805 | 45°23’23” north | 45°51′ 59″ north | |
| Average | 45°24’08.5 north | 45°51′ 02″ north | 45°55’44” |
On Clark’s map of 1805, made while at Fort Mandan, two possible “three forks” are shown. The northernmost is at a latitude of about 45°35′ N, the other is at 44°19′ N. The latitude shown for the Three Forks of the Missouri on the Lewis and Clark map of 1806 is about 45°30′ N, on Clark’s map of 1810 it is about 45°20′ N and on the Lewis and Clark map of 1814 it is 45°10′ N.
Local Time
In the chilly pre-dawn hours of 28 July, moisture-laden air from the rain that fell the previous evening developed into fog. Before sunrise the fog had gathered and thickened over the streams and wetlands. There it clung, gray and damp, until the sun topped the hills and mountains to the northeast and began to burn it off. By about 8 a.m. the fog was gone and the sun stood alone in a clear sky. This was an invitation to Lewis to take the Equal Altitudes observations that could yield his chronometer’s error on Local Time. Lewis began these observations about 8:40 by his chronometer when the sun’s upper limb reached an altitude of 72°08’15”[2]The altitude of the sun actually was about 35°58’45”. This altitude is derived from 78°08’15—8’45” (sextant’s index error) = 71°59’30” ˜ 2 … Continue reading as measured by his sextant with the artificial horizon. About a minute and a half later the sun’s center reached that same altitude, then its lower limb. With these times noted, the AM part of the observations was complete.
Storm clouds began moving into the Three Forks area from the west by early afternoon. By the time the sun had descended nearly to the altitude observed for it that morning, clouds were drifting near it. Lewis, however, was able to observe the sun’s lower limb when it had descended to a sextant altitude of 72°08”15″ above the horizon. When the sun’s center reached that altitude, clouds partially blocked it, and Lewis considered this observation: “doubtful.” A minute and a half later when the sun’s upper limb should have reached that altitude, clouds completely obscured it: “lost by clouds” Lewis wrote. He, therefore, may have doubted the usefulness of the Equal Altitude observation made that day. On 29 July, Lewis again took Equal Altitude observations of the sun. Observing conditions that day were near-perfect.
Despite the interference from afternoon clouds on 28 July, the Equal Altitude observations for that day provide all the information needed to determine the chronometer’s error on Local Time. The chronometer’s error could be found by two different methods: 1) standard Equal Altitudes calculation and 2) that outlined in Patterson’s Astronomy Notebook (1803) which Lewis carried.
- The three AM observations were reliable. This is shown by the time interval between them (1m 33s and 1m 32s). Despite the afternoon clouds, the time interval between when the lower limb and center reached the altitude of the AM observations was 1m 35. This difference is well within the acceptable range for these observations. The chronometer times for the sun’s center, AM and PM, thus, can be used to make the standard Equal Altitudes calculation for chronometer error.
- As noted above, the interval times for the AM observation were highly consistent, indicating a quality observation. Lewis also had obtained the sun’s altitude for that observation. By making a good estimate of his longitude, he could obtain a reasonable approximation of the sun’s declination. Then, by the method outlined in Patterson’s Astronomy Notebook (Problem 3, Form III), he could have calculated the true time of the observation.
Either method would have provided Lewis with the chronometer’s error. Method 1 would have given Lewis the time that the chronometer would have shown at Local Apparent Noon, and from this he could have determined its error on Local Apparent Time and Local Mean Time at noon. Method 2 would have given Lewis the Local Apparent Time of the AM observation, and from this he could have determined its error both on Local Apparent Time and Local Mean Time for that observation.
Lewis would still need to know how many seconds per day his chronometer is losing. The Equal Altitudes observation that he took on 29 July not only would have provided him with the chronometer error on Local Time for that noon, but by subtracting the noon error on the 29th from that determined for noon the 28th (or for the time of the AM Equal Altitudes observation), he could have determined the chronometer’s daily rate of loss both on Local Apparent Time and Local Mean Time. This done, Lewis has the time information he would have needed to make his calculations for longitude and magnetic declination.
| Date 1805 | Error at Local Noon Local Apparent Time |
Error at Local Noon Local Mean Time |
|---|---|---|
| 28 July | 0h 33m 39.5s fast | 0h 27m 35.4s fast |
| 29 July | 0h 33m 11.0s fast | 0h 27m 08.2s fast |
| Daily loss | 0h 00m 28.5s | 0h 00m 27.2s |
The calculations for the chronometer’s daily rate of loss, shown above, were made from Lewis’s Equal Altitudes observations. Lewis’s chronometer, however, seems to have had an irregular diurnal rate of loss. Calculations made for the time of the AM and PM Equal Altitude observations on 28 July and 29 July,[3]Using Patterson’s Astronomy Notebook (1803), Method 3, Form III. show a rate of loss of about 1 minute per day. These rates, however, require that the chronometer’s loss rate slow to only 15.6 seconds per day between the PM observation on 28 July and the AM observation on 29 July.[4]It is possible that Lewis changed his practice of winding the chronometer at noon—at least on those days when he took Equal Altitude observations—until after the PM observation was completed so … Continue reading
When the time of the lunar observations are calculated from the noon-noon chronometer errors for 28 July and 29, they are 5, 6 and 9 seconds earlier, respectively, than those calculated from the AM and PM Equal Altitudes observations (using latitude, and sun’s declination and altitude). At 4 minutes per degree of longitude this makes a longitude difference of 1’15”, 1’30” and 2’15”, respectively. The effect of these time differences on the calculated magnetic declination is less than that which most magnetic compasses can distinguish.
Lewis knew that his chronometer lost time at varying rates. If he had the opportunity, and the weather cooperated, he should have taken Equal Altitudes observations before and after Lunar Distance observations. If expedition priorities prevented his taking an Equal Altitudes observation the next day after a Lunar Distance observation, he could have taken an observation such as that noted in Method 2, above.
Longitude
Aboard merchant and naval ships from the late 1700s to the late 1800s, when several observers and several sextants were available, Lunar Distance observations were well orchestrated. The method was as follows: One observer measured the angular distances betwween the moon and sun or star and another observer recorded the time of the measurements. A third observer (and sometimes a fourth) measured the altitude of the two bodies at the beginning, end and sometimes the midpoint of the Lunar Distance observations. The times for these observations also were recorded. The altitudes obtained then were averaged to the middle time of the measurements for angular distance. The altitude of each body thus derived was called its sextant altitude and had to be corrected for index error, dip of the horizon, and semidiameter (except for a star). This gave the apparent altitude of the center of the body at the middle time of the observation. The apparent altitude then was corrected for refraction and parallax to give the true altitude of the body observed. Both the true altitude and the apparent altitude of the bodies were needed for the longitude calculations.
Lewis and Clark, however, had just one sextant and they observed only the angular distance between the moon and the sun or star. Thus the true altitude of the moon and the sun or star had to be calculated by a method such as that outlined in the Fourth Problem of Robert Patterson‘s Astronomy Notebook. The calculation involved using a) the latitude of the place of observation, b) the hour angle of the moon and sun or star, and c) the declination of the moon and sun or star. The apparent altitude then had to be determined in reverse from the calculated true altitude.
- Latitude: The latitude usually was calculated from one or more Meridian Observations of the sun.
- Hour Angle: The hour angle of the sun came from the corrected Local Apparent Time of the observation (see Local Time) and was the number of hours, minutes and seconds of the observation before or after solar noon.
The hour angle of the moon or star was calculated from 1) the corrected Local Apparent Time of the observation, 2) the right ascension of the sun and 3) from the right ascension of the moon or star. - Right Ascension and Declination: The right ascension and declination of the moon or sun were obtained by proportioning their right ascension and declination (given at Greenwich Apparent Noon in the Nautical Almanacs of the era) to the estimated Greenwich Time of the observation. The Greenwich Time of the observation was obtained from the longitude, which in turn was derived by dead-reckoning or by estimate of distance traveled from a point of known longitude.
The right ascension and declination of the star observed was calculated from the coordinates of that star as listed in Tables Requisite or in a similar book of tables. These coordinates usually were for the beginning of some year, say 1805. It was necessary to apply the given annual rate of change of these coordinates to the date (fraction of a year) of the observation.
Each step described above required lengthy calculations using logarithms. Logarithms for numbers and trigonometric functions of angles were tabulated in special books. Many of these tables gave logarithms only to four decimal places, which reduced the precision of the calculations. Mathematicians hoping to obtain higher precision for their calculations had to make interpolations for each number used. Occasions for making errors abounded. For these reasons a longitude derived from Lunar-Distance observation easily could be in error by ±15 arc minutes and not infrequently by as much as half a degree.
On 29 July about 4 p.m., when Lewis began the first of his two observations of the Lunar Distance from the sun, the moon was little more than a pale white sliver, three days old and about 40° above the horizon. It stood a little west of south nearly over the Madison River where the river emerges from the mountains. By the time Lewis finished his observations of the moon’s distance from Antares—the bright, reddish star in the constellation Scorpio—the moon had circled in its daily orbit just to the northwest of the Tobacco Root Mountains and stood only about 5 degrees above the horizon.
The captains made no calculations for longitude from these observations. The longitudes given below from the captains’ observation were calculated using an adaptation of the method devised by Chevalier Jean Borda in 1787.[5]Jean-Charles de Borda (1733-1799) was a French mariner, mathematician, physicist, and nautical astronomer who developed, among many other scientific and mathematical innovations, an important new … Continue reading
| Date | With | Calculated Longitude | Longitude from map interpretation |
|---|---|---|---|
| 1805 July 29 | Sun obs 1 | 111°13′ west | |
| 1805 July 29 | Sun obs 2 | 111°10′ west | |
| 1805 July 29 | Antares | 110°47′ west | |
| Average | 111°03′ west | ||
| Sun only | 111°11½’ west | 111°30’40” west |
| Error in arc minutes | Error in statute miles | |
|---|---|---|
| All 3 observations | 0°27.7′ east | 22¼ too far east |
| Sun observations only | 0°19.2′ east | 15½ too far east |
On Clark’s map of 1805, made at Fort Mandan, two possible “three forks” are shown, that farther to the northeast is at a longitude of 115°07′ W, that farther to the southwest is at 116°50′ W. The longitude for the Three Forks is shown at about 110°50′ W on the Lewis and Clark map of 1806, at 109°57′ W on Clark’s 1810 map and at 110°02′ W on the Lewis and Clark map of 1814.
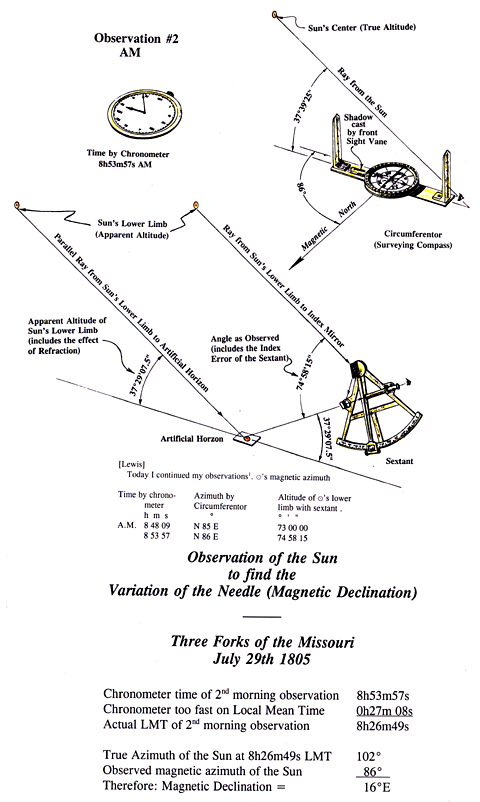
Magnetic Declination
Rain showers that fell during the evening of 28 July brought a refreshing coolness to the Three Forks valley and cleared the air of dust and haze. By the morning of 29 July the storm clouds had moved east, revealing a fair sky. Taking advantage of this situation, Lewis, early that morning, took two observations of the sun’s altitude with sextant and artificial horizon. Simultaneously, another observer (possibly Clark) took the sun’s magnetic bearing with the 6-inch-diameter surveying compass (circumferentor), and another member of the expedition recorded the times of the observations as shown by the chronometer. These observations were followed, less than ten minutes later, by the AM set of Equal Altitudes. At noon Lewis took an observation of the sun’s altitude for latitude and three and a half hours later, he took the PM set of Equal Altitudes. Less that fifteen minutes after that set of observations was complete he began the first of two separate observations of the Lunar Distance from the sun. About twenty minutes after completing the second set of observations of the Lunar Distance from the sun, the captains took another set of two observations of the magnetic bearing of the sun, its altitude and the time. Later that night, after measuring the Lunar distance from Antares, the captains also took one observation of the magnetic bearing of Polaris with the circumferentor and recorded the time of the observation.
In the early 1800s, at the latitude of the Three Forks of the Missouri, Polaris circled about 2½° from the earth’s rotational pole. Even today, though much closer to the rotational pole, Polaris is due north only twice in about 24 hours. The times when Polaris bears true north are called the upper and lower culmination. A common method of making an observation to determine the local magnetic declination by using Polaris was to find the time of upper or lower culmination of Polaris from special tables (such as Tables Requisite), correct that time for your estimated longitude (estimated Greenwich time) and make the observation at one of the times when Polaris was due north. Lewis and Clark never used this method. Instead, they took the bearing of Polaris with the circumferentor and noted the time of the observation by chronometer, often taking two or three observations several minutes or more apart. The true bearing of Polaris then had to be calculated.
| Date | With | Calculated Azimuth | Observed Azimuth | Magnetic Declination (nearest ¼°) |
|---|---|---|---|---|
| 29 July 1805 | Sun Obs 1 | 100°58′ | 085° | 16° East |
| 29 July 1805 | Sun Obs 2 | 102°02′ | 086° | 16° East |
| 29 July 1805 | Polaris | 357°42′ (-2°18′) | 013° | 15½° East[6]It would have been much more difficult to align the compass with Polaris at 45° altitude than the sun at 37° in the morning and 27° to 28° in the afternoon. |
| 1805 Average | 16° East | |||
| 1905[7]U.S. Coast and Geodetic Survey, 1905, Lines of equal magnetic declination and of equal annual change in the United States for 1905, scale 1:7,000,000 | 20° East | |||
| 1955[8]National Oceanic and Atmospheric Administration, Declination calculator. http://www.ngdc.noaa.gov/geomag/declination.shtml | 18½° East | |||
| 2005[9]ibid. | 13¾° East |
Notes
| ↑1 | This is the value Lewis recorded in 1804 in his journal entry for 22 July 1804 (see Moulton, Journals 2:411) and again in the Fort Clatsop Miscellany (Ibid., 6:496). Even though Lewis left no calculations for us to evaluate, by calculating in reverse from the latitude Lewis derived, it is possible to determine the index error he must have used for these calculations. Lewis’s calculated latitude for 29 July 1805 = 45°23’23”. |
|---|---|
| ↑2 | The altitude of the sun actually was about 35°58’45”. This altitude is derived from 78°08’15—8’45” (sextant’s index error) = 71°59’30” ˜ 2 (because of the use of an artificial horizon) = 35°59’45” minus about 1′ for the combined effects of refraction + parallax = 35°58’45”. |
| ↑3 | Using Patterson’s Astronomy Notebook (1803), Method 3, Form III. |
| ↑4 | It is possible that Lewis changed his practice of winding the chronometer at noon—at least on those days when he took Equal Altitude observations—until after the PM observation was completed so as not to affect the chronometer’s rate. Lewis recorded that the chronometer “went from 3 to 4 seconds slower in the last 12 h, than she did the first 12 h. after being wound up [emphasis added].” Moulton, Journals, 2:412. |
| ↑5 | Jean-Charles de Borda (1733-1799) was a French mariner, mathematician, physicist, and nautical astronomer who developed, among many other scientific and mathematical innovations, an important new method for measuring an arc of a meridian. He also devised a series of new trigonometric tables in conjunction with his own innovative surveying techniques. During the American Revolution, as an officer in the French Navy he commanded a fleet of six ships that saw action against the British in behalf of the United States. |
| ↑6 | It would have been much more difficult to align the compass with Polaris at 45° altitude than the sun at 37° in the morning and 27° to 28° in the afternoon. |
| ↑7 | U.S. Coast and Geodetic Survey, 1905, Lines of equal magnetic declination and of equal annual change in the United States for 1905, scale 1:7,000,000 |
| ↑8 | National Oceanic and Atmospheric Administration, Declination calculator. http://www.ngdc.noaa.gov/geomag/declination.shtml |
| ↑9 | ibid. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.