After Lewis had completed his Station Camp Observations, the celestial data would need to interpreted to determine their location.
Ocean in View?
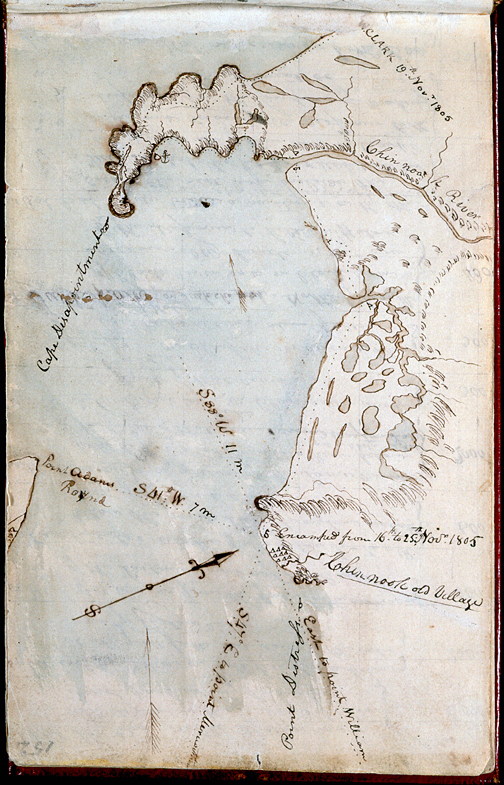
Although this map is labled “ca. November 16-25” in Moulton (6:52), Clark probably drew it sometime during the winter of 1806 from the field notes he made in November (see Moulton, Atlas, Maps 90-93). For one thing, the almost incessant rain and wind they endured from the time they left Station Camp until the captains moved into their quarters at Fort Clatsop on 23 December 1805 would have prevented Clark from preparing such a detailed chart, with its water tinted blue. Moreover, “Point William” (today, Tongue Point) did not acquire that name until 27 November 1805 (Moulton, 6:90). His “Point Lewis” is now Smith Point, at the west end of Astoria, Oregon, and slightly east of the mouth of Youngs Bay. “Point Distress” is now Point Ellice, Washington. The distance from Station Camp to Cape Disappointment would actually have been 6.9 miles, not 11; his 7-mile estimate of the distance to Point Adams would have been more accurately 3.8 miles. See also Ocean in View?.
By noon, 18 October 1805, Meriwether Lewis had completed his celestial observations, and William Clark had measured the width of the Snake and Columbia Rivers. Lewis then completed recording a vocabulary of primal words in the local languages. This done, the expedition launched its canoes and headed downstream on the Columbia River. Two hundred river miles—and several portages—brought them to Pacific tidewater near Beacon Rock on 2 November 1805.
Five days later, 7 November 1805, the party reached a rock 20 feet in diameter rising more than 50 feet above the river level; it stood about one-half mile from the river’s north shore. From an unspecified location near this pillar of rock, William Clark focused his gaze downstream to the west along the course of the Columbia River. What he saw there prompted him to record: “Great joy in camp we are in View of the Ocian.” Strangely, Clark’s journal is the only one to express this joy. Ordway, on 8 November 1805, simply records: “we can See along distance ahead we expect we can see the mo. Of the Columbia River . . . but it appears a long distance off.”
Clark’s journal entry has engendered considerable discussion. What did he see that prompted this entry? Although this was not a celestial observation, it merits treatment here.
Clark did not see the Pacific Ocean—its eastern shore lies about 20 miles west of Pillar Rock. Because of the earth’s curvature,[1]Refraction has the apparent effect of reducing the earth’s curvature. A common equation for the combined effects of earth’s curvature and refraction, in feet, is: 0.574 x mile. Example: … Continue reading the horizon that Clark would have seen from near Pillar Rock (assuming that he was standing up and looking west) would have been only about 3 miles distant; that is, just southeast of Grays Bay. In order to have seen the ocean, itself, Clark would have needed to climb the rain-soaked hills on the mainland north of Pillar Rock, ascending them to a height of about 230 feet above the river—that is, he might have seen the ocean provided that the fog had lifted by then, and the rain had stopped. Nevertheless, the geographic setting of the expedition’s route for the latter part of 7 November provides some clues to what Clark saw or thought he saw. About 5 miles upstream (eastward) from Pillar Rock the Columbia River, in its seaward course, makes an abrupt bend from northwest (azimuth 325°) to just south of west (azimuth 260°). This bend marks the upstream end of the river’s estuary and, from that point, the Pacific Ocean lies about 32 miles to the west. Hills.[2]The hills to the north were near Point Ellice, Washington (the highest is more than 1100 feet above sea level); those to the south were just east of Astoria, Oregon (the highest is more than 600 feet … Continue reading border the north and south sides of the estuary. As seen from Pillar Rock, however, the hills that are near the north and south ends of the present-day Astoria Bridge hide those hills that are farther west. And, as seen from near Pillar Rock this effect creates a 4-mile-wide span of true horizon. This 4-mile-wide span of horizon may have suggested to Clark that he was seeing the ocean . . . or at least, the direct opening to it. Therefore, although the ocean—the expedition’s long-sought goal—still lay unseen below the horizon from near Pillar Rock, Clark’s sixth sense of geography must have told him there was open water all the way to it. Joy indeed . . . though short lived!
Station Camp Observations
Continuing west on the morning of 8 November, the expedition’s canoes generally hugged the northern shore of the Columbia’s estuary around Grays Bay. That evening they made camp near present-day Portuguese Point. High winds and waves kept them from traveling on the 9th, but on the 10th they continued about 7 miles generally southwest to a small cove about 1 mile northeast of present-day Point Ellice, Washington. Rain, hard winds and billowing waves pinned them to the narrow beach from 10 November and to the afternoon of 15 November, eliciting the name Camp Distress for this stopping place. Lewis and a small scouting party set out from Camp Distress on 13 November to explore the area west to the ocean while Clark remained in charge of the camp. In the afternoon of the 15th, after the wind abated, Clark set out with the canoes. Fighting the waves for about one-half a mile, he rounded Point Ellice. He then continued about 2 miles west-northwest to a small sand beach near present-day McGowan, Washington. There, where a small stream ran down from the hills, he made camp. The captains later dubbed it Station Camp.
The center of the mouth of the Columbia (as projected from the headlands to the north and south of the river’s estuary) on the following maps is shown at the following coordinates:
| Map | Date | Latitude, Longitude | Gt. Circle Initial Azimuth* | Statute Miles* |
|---|---|---|---|---|
| Nicholas King | 1803 | 46˚15’N, 123˚45’W | 088 | 12.4 mi |
| William Clark | 1805 | 46˚15’N, 123˚36’W | 089˚ | 19.6 mi |
| Lewis and Clark | 1806 | 46˚20’N, 123˚36’W | 072˚ | 20.5 mi |
| Robert Frazer | 1807 | 46˚50’N, 125˚00’W | 311˚ | 62.4 mi |
| William Clark | 1810 | 6˚15’N, 124˚54’W | 271˚ | 42.7 mi |
| Lewis and Clark | 1814 | 46˚20’N, 124˚54’W | 278˚ | 43.1 mi |
| present-day | 46˚15’N, 124˚00’W*** |
*Initial heading from the mid-point between Point Adams and Cape Disappointment.
** Great Circle distance from mid-point between Point Adams and Cape Disappointment
*** Coordinates are for the mid-point between Point Adams and Cape Disappoint as shown on U.S. Geological Survey 1:24,000 map; 5.7 miles apart.
Clouds, fog and rain prevailed over clear skies while the expedition remained at Station Camp. On those few days when weather permitted, however, the captains took celestial observations. These were the last observations they obtained in 1805, and were the only ones they made for longitude on the coast.
The following are the observations that they recorded while at Station Camp 15–24 November 1805; all data are from Clark:
| Map | Date | Latitude, Longitude | Gt. Circle Initial Azimuth* | Statute Miles* |
|---|---|---|---|---|
| Nicholas King | 1803 | 46˚15’N, 123˚45’W | 088 | 12.4 mi |
| William Clark | 1805 | 46˚15’N, 123˚36’W | 089˚ | 19.6 mi |
| Lewis and Clark | 1806 | 46˚20’N, 123˚36’W | 072˚ | 20.5 mi |
| Robert Frazer | 1807 | 46˚50’N, 125˚00’W | 311˚ | 62.4 mi |
| William Clark | 1810 | 6˚15’N, 124˚54’W | 271˚ | 42.7 mi |
| Lewis and Clark | 1814 | 46˚20’N, 124˚54’W | 278˚ | 43.1 mi |
| present-day | 46˚15’N, 124˚00’W*** |
The results of these observations follow.
Latitude
The morning of the 16th dawned “Clear and butifull,” but “the wind was hard from the S W.” At noon Clark took advantage of the conditions and made an observation of the sun’s altitude for latitude. He used the sextant and artificial horizon:
I took a meridian altitude with sextant 50°36‘15“; the shaking image below
Clark’s “shaking image” most likely refers to the image of the sun reflected from the artificial horizon. The artificial horizon—in this case a tray nearly filled with water—was set in a shallow excavation so that the water surface was at or slightly below ground level. A wind screen or housing then was placed over the tray, but not touching it, to help reduce the effect of wind on the water surface. Nevertheless, the strong southwest wind must have produced a slight oscillation of the water surface, causing the image to shake. In spite of that, Clark’s observation at Station Camp was one of his best.
| Latitude that Clark calculated from his Meridian Altitude of the Sun | 1805 November 16 | 46˚19’11.1" |
| Latitude recalculated from Clark’s Meridian Altitude of the Sun | 1805 November 16 | 46˚15’47.3" |
| Difference | 00˚04’23.8" |
The difference of 4‘ 24“ between the recalculated latitude and that which Clark calculated comes from the incorrect method he and Lewis used to calculate latitude from an observation using the sextant and artificial horizon. The captains subtracted the index error of 8‘45‘ after they divided the observed angle by two; they should have either: 1) subtracted the sextant error before they divided by two or 2) subtracted half the error after dividing by two. This error makes the captains’ calculated sextant-artificial horizon latitudes too far north by an average of 4‘ 22½“ (5 statute miles).
As interpreted from Clark’s maps and from the expedition’s courses and distances, Station Camp was at 46°14‘ 47“ North Latitude—just 1 arc minute south the latitude recalculated from Clark’s meridian observation. A latitude error of 1 arc minute (1.15 statute miles) from a sextant observation was within the normal limits of accuracy for that time. This shows that, despite the “shaking image,” Clark’s observation was a good one. Note, however, that if an index error of +6‘ 45“ is used for the sextant instead of +8‘ 45“, it produces a latitude of 46°14‘ 48“ for this observation—just 1 arc second north of the actual latitude.
Sextant Error
Having introduced, in the paragraph above, the suggestion about a different index error for the sextant, this seems like a opportune place to discuss its index error. All celestial observations that Lewis and Clark took with their sextant, except the Equal Altitudes observation, need to be adjusted for the sextant’s index error. Whereas an index error of a minute or so, when using an artificial horizon, does not greatly affect the latitude, magnetic declination or even the time calculated for that observation, it makes a substantial difference in the calculated longitude. From November 1803 when the expedition was at the mouth of the Ohio until November 1805 on the Pacific, the captains recorded that the sextant index error was 8‘ 45“ subtractive. That is, the sextant read too high by 8‘ 45“ and that amount had to be subtracted from all observations. A sextant’s index error, however, rarely remains the same for a long time, and most navigators routinely check the index error of their instruments. Lewis may have done so, but never recorded any change in the sextant’s index error until February 4, 1806. On that date he gave its index error as 5‘ 45“ subtractive (too high). Longitudes calculated from Kansas River Observations, Fort Mandan Observations, Marias River Observations, Missouri Headwaters Observations, Fortunate Camp Observations, and Clearwater Canoe Camp Observations suggest that if the sextant’s index error had changed, it had not changed significantly. Although calculated longitudes generally are too far east of the actual longitude by 15—20 arc minutes this may result as much from observing error as from the sextant’s index error. Beginning at the mouth of the Snake River, however, the longitude calculated from the captains’ observations seem to indicate that the sextant’s index error had changed, perhaps by an arc minute or more. Unfortunately, without reliable chronometer times the true index error cannot be ascertained.
Local Time
Fair and cool weather greeted Clark at Station Camp on the morning of 17 November. Because Lewis still had not returned from exploring the coast west of that camp, Clark took it upon himself to make the AM observations for Equal Altitudes of the sun. Lewis returned to camp about 1 PM, but it probably was Clark who completed the PM Equal Altitude observations. After correcting for two mistakes that Clark’s assistant made in reading the chronometer that morning, these observations give the chronometer error at solar noon.[3]Given a clock time of 12 noon on 17 November, one could designate that time Day 17.5; similarly, 9 PM on that day could be called Day 17.875. Decimal time is useful when comparing chronometer loss … Continue reading
| Date | Error on Local Apparent Time | Error on Local Mean Time |
|---|---|---|
| 17 November 1805, noon: | 15m 56s slow | 1m 19s slow |
Adverse weather prevented the captains from taking celestial observations for longitude until 24 November. To make reliable longitude calculations from the Lunar Distance observations, accurate time is needed for those observations. If the expedition’s chronometer had kept perfect time or always had run at a steady rate, the time of the Lunar Distance observations could be projected reliably from 17 November to the observations on the 24th. The captains knew that their chronometer did not run at a steady rate; they also knew that sometimes it stopped. They needed another observation or set of observations from which the true time could be calculated to find the chronometer’s error on Local Time.
On the morning of 24 November 1805 the captains began taking observations for Equal Altitudes of the sun and completed them a few minutes later. Clouds, however, blocked the sun in the afternoon, preventing the captains from taking the PM observations. Although Clark recorded the times for the AM observations, he—perhaps thinking that without the PM observations the AM data were unuseable—failed to record the sun’s altitude for the AM observations. If Clark HAD recorded the sun’s altitude for the AM observations, a good value for the chronometer’s error could have been calculated despite the missing PM data. As such, this Equal Altitudes observation cannot be used to help determine the time of the Lunar Distance observations.
Shortly before the AM Equal Altitudes observation on 24 November 1805 the captains took an observation of the sun for Magnetic Declination. Clark dutifully recorded the chronometer times and sun’s magnetic bearing and its altitude. Unfortunately, Clark failed to record whether Lewis had observed the sun’s upper limb, its lower limb or its center. If Clark had recorded this information, the chronometer’s error on Local Time for this observation easily could have been calculated by using Robert Patterson‘s Problem 3, Form III. In November, at the latitude of Station Camp and time of day this observation was made, the sun’s altitude increases by one semidiameter in a little more than two minutes. Calculations for the time of the observation made assuming the altitude recorded was for the lower limb would differ by more than four minutes from those made assuming the altitude was for the upper limb—and four minutes makes a difference of one degree of longitude.
Does this mean that the observations the captains made for longitude are unuseable?
No . . . times for the Lunar Distance observations still can be approximated, but the confidence level for the accuracy of the longitudes derived is not high.
Methodology
The method I used to determine the time for the longitude observations is lengthy, but could have been made by mathematicians of the early 1800s. It is summarized as follows:
- Determine the chronometer error at Local Apparent Noon on 17 November from the Equal Altitudes observations taken that day (this value is shown in Table 4, above).
- Calculate the Local Apparent Time of the observation for Magnetic Declination; assume that it was the upper limb that was observed (see discussion, below and Magnetic Declination, below),
- Subtract the average chronometer time of the Magnetic Declination observation from the calculated time of theobservation average; this gives the minutes and seconds that the chronomieter is slow on Local Apparent Time,
- Determine the Equation of Time for the observation for Magnetic Declination and subtract it from the chronometer’s error on Local Apparent Time; this gives the minutes and seconds that the chronometer is slow on Local Mean Time,
- Subtract the result of Step 1 from the result of Step 4; the result is the minutes and seconds of Mean Time that the chronometer lost between the two observations,
- Divide the result of Step 5 by the number of hours of Mean Time that elapsed between the two observations; this gives the chronometer’s hourly rate of loss on Local Mean Time, which will essentially be that for Local Apparent Time for the date in question.
- Find the difference in time between the Lunar Distance observation average and that of the Magnetic Declination average, multiply the result by the result of Step 6; this gives the number of additional seconds that the chronometer has lost since the observation for Magnetic Declination,
- To the result of Step 8, add the number of minutes and seconds that the chronometer was slow on Local Apparent Time for the observation for Magnetic Declination (this value was found in Step 3); this gives the chronometer’s total error on Local apparent Time for the Lunar Distance observation with the sun,
- Add the result of Step 8 to the chronometer time of the Lunar Distance observation with the sun; this gives the calculated Local Apparent Time of the observation average.
- Repeat Steps 7-9 for the Lunar Distance observation with Markab.
Lower or Upper Limb?
Between the mouth of Ohio River and Long Camp the captains made twenty-eight observations of the sun for Magnetic Declination. Of these, they specifically recorded only one as being of the sun’s center. For five observations, including that of 24 November 1805, they did not specify which limb was observed. Eleven of the observations they recorded as being of the sun’s upper limb and eleven were of the sun’s lower limb. For those observations of the sun’s lower limb, however, the lowest sun altitude was more than 2° higher than the lowest of the three sightings made on 24 November. Inasmuch as the sun on 24 November was only about 11° above the horizon for the average time of the three timed observations for Magnetic Declination, it is not likely that the captains observed the sun’s lower limb. Good observation practice suggests that the captains observed the upper limb.
The chronometer’s daily rate-of-loss of about 33 seconds per day while at the mouth of Snake River lends additional support to the interpretation that Lewis observed the sun’s upper limb for the Magnetic Declination observation of 24 November.
Longitude
Rain and clouds! . . . clouds and rain! . . . day after day since 17 November. Finally, on the morning of 24 November the sky was fair once more. The captains took observations of the sun for magnetic declination, then took the AM observation for Equal Altitudes of the sun to check the chronometer’s error on Local Time. The sky remained clear until about 3:00 p.m. Local Time, allowing the captains to measure the angular distance between the moon and the sun, but clouds cove the sun before the PM Equal Altitudes observations could be taken. The sky clea sufficiently after dark to permit the captains to measure the angular distance between the moon and the star Markab (![]() Pegasi), the brightest star in the constellation Pegasus, at about 8:30 p.m.
Pegasi), the brightest star in the constellation Pegasus, at about 8:30 p.m.
Because the captains could not complete the PM Equal Altitudes observation, and—worse!, because Clark failed to record the already-measured sun’s altitude for the AM observation—the chronometer’s error on Local Time and its daily rate of loss cannot be calculated from that observation.The chronometer’s error at the time of observation can be determined to a satisfactory degree of accuracy, however, by calculating the time of the observation for Magnetic Declination on 24 November (see previous page Local Time).
Assuming the Sun’s Upper Limb was Observed for Magnetic Declination Longitude resuts Extending Line A-B-C-D to the Times of Observation:
| 1805 Date | With | Calculated Longitude | Actual Longitude | Error in ° ‘ | Error in statute miles (47.75 mi per° at 46°16′) |
|---|---|---|---|---|---|
| Nov 24 | Sun | 122°15‘W. | 123°54½‘ W. | 1°39½‘ E. | 79 |
| Nov 24 | Markab | 123°26‘ W. | 123°54½‘ W. | 0°28½‘ E. | 23 |
Assuming the Sun’s Center was Observed for Magnetic Declination:
| 1805 Date | With | Calculated Longitude | Actual Longitude | Error in ° ‘ | Error in statute miles (47.75 mi per° at 46°16′) |
|---|---|---|---|---|---|
| Nov 24 | Sun | 121°54‘ W. | 123°54½‘ W. | 2°00½‘ E. | 96 |
| Nov 24 | Markab | 122°31‘ W. | 123°54½‘ W. | 1°23½‘ E. | 66½ |
Table 5 clearly shows that the calculated longitudes are closer to the actual longitude when using the time of the sun’s upper limb from the observation for magnetic declination, rather than the time of its center.
Usually, the expedition’s Lunar Distance observations with the sun yield longitudes nearer to the actual longitude than those with stars. The Lunar Distance observation with Markab at Station Camp, however, yields a longitude that is more than a degree nearer to the actual longitude than the observation with the sun. Was the observation with Markab simply a much better observation than that with the sun?
On February 4, 1806, Lewis recorded that the sextant’s index error was 5’45” subtractive (that is, it read 5’45” too high). Suppose the sextant’s index error was NOT +8’45” but +5’45” . . . how would that affect the longitude calculated?
Using times produced by projecting the chronometer error obtained in Step 6 of the section LOCAL TIME for the Lunar Distance observations:
| For the Moon-Sun observation the resultant longitude is | 123°50′ W |
| For the Mon-Markab observation the resultant longitude is | 121°45‘ W |
As can be seen from the above, using an index error of 5‘45“ (both for the Lunar Distance observations and the calculated time of those observations) results in a Moon-Sun longitude that is within 5 arc minutes of what it should be. On the other hand, it moves the Moon-Markab longitude much too far to the east.[4]This reversal of calculated longitudes happens because with the moon-sun observations the angular distance between the near limbs is measu. At the time of the Moon-Markab observations, however, only … Continue reading
Declination (Variation of the Compass Needle)
Beginning about 8:30 a.m. (chronometer time), 24 November 1805 Lewis took three observations of the sun’s altitude with his sextant and the artificial horizon. Simultaneous with Lewis’s observations Clark, using the 6-inch-diameter circumferentor, took the magnetic bearing of the sun. Additionally, an assistant recorded the chronometer’s time for each observation.
Clark, in his journal for 24 November 1805 recorded the three altitudes, bearings and times. He failed, however, to record whether Lewis observed the sun’s upper limb, lower limb or its center, and Lewis left no data regarding this observation for Magnetic Declination. From the sun’s altitude at the time of observation and evaluations made to determine Local Time for the Lunar Distance observations (see Local Time at Station Camp), the limb observed most likely was the upper. The sun’s true altitude at the time of observation, however, was calculated for the upper limb, the center and lower limb to evaluate the differences.
After averaging the sun’s altitude from the three observations, the sun’s true altitude was calculated for the upper limb, center and lower limb using:
- a sextant’s index error of +8°45‘ and,
- a longitude of 123°45‘ W to adjust the sun’s semidiameter (for upper and lower limbs) from the 1805 Nautical Almanac.
The Local Apparent Time of the Magnetic Declination observation then was calculated from the sun’s true altitude(s) using:
- the latitude of Station Camp recalculated from the Meridian Observation of 16 November 1805 and,
- a longitude of 123°4‘ W to adjust the sun’s declination from the 1805 Nautical Almanac.
- Patterson’s Problem 3, Form III (1803).
Assuming the Sun’s Upper Limb was observed:
| Recalculated latitude: | 46˚15’47.3" N |
| True altitude of sun’s center | 11˚13’02.4" |
| Sun’s declination at observation: | 20˚35’25.6" S |
| Calculated Apparent Time of the observation: | 8:55:32.2 |
| Calculated azimuth of the sun: | 136˚32’27" |
| Average bearing of the sun, S63˚E = azimuth of: | 117º |
| Magnetic Declination from observation average: | 019˚32’27" E = 19½˚ East |
Assuming the Sun’s Center was observed:
| Calculated Apparent Time of the observation: | 8:57:49.4 |
| Calculated azimuth of the sun: | 137˚00’51" = 20˚ East |
Assuming the Sun’s Lower Limb was observed:
| Calculated Apparent Time of the observation: | 9:00:07.8 |
| Calculated azimuth of the sun: | 137˚29’15" = 20½˚ East |
| Clark, 24 November 1805 (Moulton, volume, p. 84): | 16˚ East |
| 1805 calculated from captains’ observation, upper limb: | 19½˚ East |
| 1905[5]U.S. Coast and Geodetic Survey, 1905, Lines of equal magnetic declination and of equal annual change in the United States for 1905, scale 1:7,000,000 | 22½˚ East |
| 1955[6]National Oceanic and Atmospheric Administration, Declination calculator. http://www.ngdc.noaa.gov/seg/geomag/struts/calDeclination | 21¾˚ East |
| 2005[7]Ibid. | 17½º East |
Comparing the bearings shown on that map with bearings from true North derived from modern maps gives the following magnetic declinations for 1805:
| From | To | Declination |
|---|---|---|
| Station Camp | Tip of Cape Disappointment | 20˚ East |
| Station Camp | Point Adams | 2˚ East[8]At a magnetic declination of 19½° East, Clark should have read a bearing of about S21°W, not S41°W, from Station Camp to Point Adams. |
| Station Camp | Meriwethers Point | 19½˚ East |
| Station Camp | Point William | 17¾˚ East |
| Average (disregarding Station Camp to Point Adams) | 19˚ East | |
Notes
| ↑1 | Refraction has the apparent effect of reducing the earth’s curvature. A common equation for the combined effects of earth’s curvature and refraction, in feet, is: 0.574 x mile. Example: distance 20 miles; 0.574 x 202 = 0.574 x 400 = 230 feet. This means that, at a distance of 20 miles, an object would have to rise at least 230 feet above the eye of the observer to be seen. The inverse of this equation is: 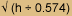 = miles to horizon. Example: eye height 5.5 feet; 5.5 ÷ 0.574 = 9.582, take the square root of 9.582 = 3.1 miles. This means that for an observer whose eye is 5.5 feet above the ground the true horizon is 3.1 miles away. = miles to horizon. Example: eye height 5.5 feet; 5.5 ÷ 0.574 = 9.582, take the square root of 9.582 = 3.1 miles. This means that for an observer whose eye is 5.5 feet above the ground the true horizon is 3.1 miles away.The effect of refraction is dependant principally upon the temperature and density of the air between the object viewed and the observer. An air mass of anomalous temperature or density sometimes can form a lens that will produce a mirage in which objects that are below the horizon appear to be elevated above it. Given the prevalent weather conditions on 7 November 1805 and the distance to the ocean, however, this situation would have been most unlikely. |
|---|---|
| ↑2 | The hills to the north were near Point Ellice, Washington (the highest is more than 1100 feet above sea level); those to the south were just east of Astoria, Oregon (the highest is more than 600 feet above sea level). |
| ↑3 | Given a clock time of 12 noon on 17 November, one could designate that time Day 17.5; similarly, 9 PM on that day could be called Day 17.875. Decimal time is useful when comparing chronometer loss rates over several days, especially when used with linear regression capabilities on modern hand-held calculators. |
| ↑4 | This reversal of calculated longitudes happens because with the moon-sun observations the angular distance between the near limbs is measu. At the time of the Moon-Markab observations, however, only the western limb of the moon was illuminated whereas Markab was east of the moon. Lewis, thus, had to measure the angular distance from Markab to the moon’s far limb instead of its near limb. The smaller index error (in this case) makes the calculated longitude from the moon-sun distance farther west, but makes the moon-Markab longitude farther east. |
| ↑5 | U.S. Coast and Geodetic Survey, 1905, Lines of equal magnetic declination and of equal annual change in the United States for 1905, scale 1:7,000,000 |
| ↑6 | National Oceanic and Atmospheric Administration, Declination calculator. http://www.ngdc.noaa.gov/seg/geomag/struts/calDeclination |
| ↑7 | Ibid. |
| ↑8 | At a magnetic declination of 19½° East, Clark should have read a bearing of about S21°W, not S41°W, from Station Camp to Point Adams. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.