After Lewis had completed his Fortunate Camp observations, the celestial data would need to interpreted to determine their location.
Fortunate Camp, as Lewis and Clark described it, was at the forks of the Jefferson River, for them the farthest point of navigation on the Missouri. It was there that they laid up their canoes and, having had the good fortune to meet the Lemhi Shoshone and barter for horses, proceeded on more than 300 miles overland, crossing several mountain ranges, until they reached the forks of the Clearwater River in present-day Idaho.
The names that the captains gave these streams—East Fork and West Fork Jefferson River—do not appear on modern maps. Where were the forks of the Jefferson River?
Several means are available to resolve the question. The earliest known “investigators” were several perceptive fur trappers in the late 1820s and early 1830s, such as Warren Ferris, John Work, and Alexander Ross. Their method of identifying features that Lewis and Clark described was simply to read the 1814 edition of the journals and match the captains’ descriptions with the geography they saw for themselves. By the 1830s the Jefferson River above its junction with the present-day Big Hole River and Ruby River already was called the Beaverhead River, and fur trappers had given the east fork of the Beaverhead River its modern name, Red Rock River. The west fork was first called Horse Plains presumably because Lewis and Clark traded for horses there with the Shoshones; its name was changed around 1865 to avoid confusion with another Horse Plains in northwestern Montana.
But how certain can we be that the identifications made by the mountain men were correct?
The simplest and surest way to identify these forks is to review Clark’s maps and compare them with modern maps. Another way is to plot the expedition’s river and route-survey data and compare the plot with modern maps. Both methods have been used, and they confirm the general location of Fortunate Camp. Additionally, by using maps and aerial photographs that pre-date the reservoir now covering the campsite, it appears that the coordinates for Fortunate Camp most probably were at or near 44°59’36″N, 112°51’43″W (1927 datum). Nevertheless, an important cross-check of the camp’s location comes from an evaluation of the data that Lewis and Clark obtained from their celestial observations for latitude and longitude.
Latitude by Clark
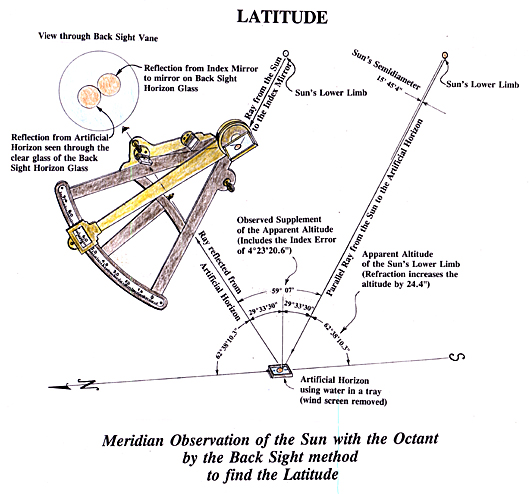
An Early 19th-century Sextant
In his journal entry for 18 August 1805, Clark recorded, “The Latd of the forks agreeable to observation is 43°30’43” North.” This is a surprising entry not only because the latitude that Clark recorded is nearly one and a half degrees (100 miles) too far south of the actual site, but also because none of the other journals mention a latitude being obtained at Fortunate Camp before the 19th—one day after Clark had left on his reconnaissance of the Salmon River. Considering the intense level of activity that must have occurred after the captains were reunited on the 17th, and their parleys and trading with the Shoshone, it is most unlikely that either captain found time to make a meridian observation. But, supposing Clark did make an observation of the sun’s altitude on the 17th (or on the 18th before he set out for his Salmon River exploration), wouldn’t Lewis have mentioned it, recording at least the observed altitude of the sun? And later, when Lewis made his own observations and found Clark’s latitude to be in error, couldn’t he have made a comment about it similar to the one he made about Clark’s observation on 15 August 1805 at Rattlesnake Cliffs?
Clark’s entry for the 18th clearly states that the latitude of the forks came from an observation. But what if an observation was not actually made at Fortunate Camp. Suppose Clark estimated it, taking the distance he traveled south from Rattlesnake Cliffs, converting it to degrees, minutes and seconds and then subtracting that from the latitude he calculated for Rattlesnake Cliffs? Although calling the derived latitude an “observation” would clearly be stretching the meaning of the word, it is still a justifiable usage.
The latitude Clark had calculated for the Rattlesnake Cliffs, unfortunately, was too far south by about one degree (69 miles), as Lewis pointed out—probably after making his own observations at Fortunate Camp. If Clark’s latitude for Rattlesnake Cliffs had been correct, he could have calculated the straight-line distance he had traveled south from the Rattlesnake Cliffs, converted that to degrees, minutes and seconds, and subtracted them from the latitude at Rattlesnake Cliffs. This means, however, that Clark would have needed to plot his river survey data before making the calculation, and it is unlikely that he had time to do so by the morning of the 18th. But supposing that the unlikely happened, and that Clark had indeed plotted his survey data, he would have found that the forks lay only 15½ miles south of the Rattlesnake Cliffs. Converting this distance into latitude would have placed the forks only about 13’30” of latitude south of Rattlesnake Cliffs, not 30 minutes, and his calculated latitude for the forks of the Jefferson would have been about 43° 47′ 18″. Therefore it is highly improbable that the latitude Clark recorded in his journal for the 18th came from a calculation like that described above.
There is another possible source of Clark’s erroneous latitude, but it involves some compounded errors plus the fact that the captains didn’t always record events on the date that they happened. On Clark’s map, east of the indicated site of Fortunate Camp is the notation: No. 43 Latd. 43°30’43” (the figure in minutes can be interpreted variously as 30′, 35′, or 38′, but most likely it is 30).[1]The “No. 43” stands for “Point of Celestial Observation Number 43,” their forty-third such point of observation since leaving Fort Mandan. A line through it indicates that Clark wished to delete it. Underneath the deleted latitude he wrote: 44°35’28.1″, which is the average of the four observations that Lewis made between 19 August 1805 and 21 August 1805.
Based on the drafting style and the notations, it seems reasonable to suggest that Clark plotted Atlas Map 65 (from the Three Forks of the Missouri to three forks of the Jefferson), Atlas Map 66 (from the three forks of the Jefferson to Fortunate Camp) and Atlas Map 67 (at least that part to the divide) while waiting at Fish Weir Camp for Lewis. On 27 August 1805, Clark received a message from Lewis to meet him at the “upper” Shoshone camp. In view of the language barrier, Lewis must have written a note for the young Shoshone messenger to deliver. Did that note contain the latitude of Fortunate Camp from one of Lewis’s observations? Lewis’s observation for the 20th yielded a latitude of 44°39’43”. The 9 of 39′ easily could have been misread for a 0, making it 30′, but the 4 of 44 would be difficult to mistake for a 3. Even if the minutes of latitude were misread from a poorly written numeral, it still takes another condition to produce the change in the degrees. One answer might be that Clark, thinking of his own observation of 15 August 1805, with its latitude of nearly 44° north, may have thought that Lewis meant 43° and changed it. Not knowing of his error, he then may have added the 30’43”, thus recording 43°30’43” on his map and in his journal, but back-dating the journal entry to the 18th because that’s where he was at the time. This is a difficult interpretation to defend, but it could have happened.
When Lewis and Clark rejoined on 29 August 1805 Lewis corrected Clark’s understanding of the latitude, and Clark dutifully changed it on his map. Why didn’t he also change it in his journal? It is likely that the journals already had been put away for safe-keeping in preparation for the resumption of the journey, and Clark forgot to change it later. At any rate, despite the uncorrected latitude in Clark’s journal, Clark’s map bears Lewis’s calculated average latitude of Fortunate Camp from four observations.
Latitude by Lewis
On 19 August, Lewis dutifully made and recorded a series of celestial observations of the sun (![]() ) and moon (
) and moon (![]() ) for longitude and a meridian[2]On the earth a meridian is any line that passes through the north and south poles and is perpendicular to the equator. The half of the meridian circle that is on the observer’s side of the … Continue reading altitude observation of the sun’s lower limb (L.L.) at noon for latitude:
) for longitude and a meridian[2]On the earth a meridian is any line that passes through the north and south poles and is perpendicular to the equator. The half of the meridian circle that is on the observer’s side of the … Continue reading altitude observation of the sun’s lower limb (L.L.) at noon for latitude:
today I observed time and distance of the ![]() ‘s and
‘s and ![]() ‘s nearest limbs with sextant[3]Lewis’s sextant was in the form of an arc encompassing one-sixth of a circle, hence the name sextant. Because a sextant uses an index mirror to reflect objects to a second mirror and then into … Continue reading
‘s nearest limbs with sextant[3]Lewis’s sextant was in the form of an arc encompassing one-sixth of a circle, hence the name sextant. Because a sextant uses an index mirror to reflect objects to a second mirror and then into … Continue reading ![]() East. it being the Point of Observation No. 43
East. it being the Point of Observation No. 43
| Time (A.M.) | Distance |
|---|---|
h m s |
° ' " |
11 37 11 |
65 53 15 |
" 39 50 |
" 52 15 |
" 44 15 |
" 50 45 |
" 46 18 |
" 49 – |
11 51 37 |
65 47 15 |
" 54 43 |
" 45 30 |
" 55 53 |
" 44 15 |
" 57 40 |
" 43 30 |
" 59 30 |
" 42 30 |
Observed Meridian Altitude of
‘s L.L. with Octant[4]The octant also was a device to measure the angle between two objects. Although its graduated arc spanned 45° (an eighth of a circle, hence octant) it could measure an angle of 90° (when used … Continue reading
by the back observation 69°15’00”
Latitude deduced from this observation. N. 44°37’57.4″
And, on the 20th, Lewis:
observed time and distance of the
‘s. and
‘s nearest Limbs with Sextant.
East.
| Time (A.M.) | Distance |
|---|---|
h m s |
° ' " |
11 37 11 |
65 53 15 |
" 39 50 |
" 52 15 |
" 44 15 |
" 50 45 |
" 46 18 |
" 49 – |
11 51 37 |
65 47 15 |
" 54 43 |
" 45 30 |
" 55 53 |
" 44 15 |
" 57 40 |
" 43 30 |
" 59 30 |
" 42 30 |
Longitude deduced from this observation West of Greenwich [blank—not calculated]
Latitude N. deduced from the Hor ∠[5]It appears that Lewis uses the abbreviation “Hor” to mean “horizon.” Combining it with the geometric symbol for angle creates the expression “horizon angle.” It … Continue reading of the P.M. Observation of‘s center 44° 33’ 50.5″
Observed Equal Altitudes[6]An equal altitudes observation is a two-part process. The first set of measurements is taken when a celestial object is east of the observer’s meridian and the second set is taken when the … Continue reading with Sextant of the Sun.
|
A.M. 8h 45m 30s ” 47m 04s ” 49m 40s |
P.M. 3h 55m 40s ” 57m 16s ” 58m 50s |
} | Altitude by Sextant at the time of observation 68° 30′ |
Observed Meridian Altitude of ![]() ‘s. L.L. with Octant by the back observation 70° ‘ “
‘s. L.L. with Octant by the back observation 70° ‘ “
Latitude deduced from this observation N. 44° 39′ 43″
Finally, on 21 August, Lewis:
observed Equal Altitudes of the
with Sextant.
|
A.M. 8h 38m 36s ” 40m 04s ” 40m 42s |
P.M. 4h 00m 56s ” 01m 34s ” 03m 05s |
} | Altitude at the time of observation 65° 57 ’30” |
Also observed Meridian Altd of
‘s L.L. with Octant by the back observation 72°00’00”
Latitude deduced from this observation North. 44°30’21.7″
Mean Latitude of the Forks of Jefferson’s river deduced from three observations of the Meridian Altd of the‘s L.L. with Octant, and one calculation by means of the hor: ∠ of the
‘s center in the P.M. observation for equal Altitudes on the 20th Instant N. 44°35’28.1″
Octant Observations
Lewis took three meridian altitude observations of the sun with his octant and one afternoon observation of the sun with his sextant, and from each of these observations he calculated a latitude. He then computed the mean (or average) of these observations at 44°35’28.1″ North.
If, as suggested, Fortunate Camp was at 44°59’36″N, how did Lewis, after averaging four observations, come up with a latitude 24 minutes too far south?
Although Lewis was without peer as an observer, his mathematical skills were less well-developed. Not only that, in all his latitude calculations for 1805, when he used the octant in the back observation, he employed the wrong index error.[7]The index error (sometimes called instrument error) is the angular difference between what the instrument measures and what it actually should measure if it were in perfect alignment. The error … Continue reading On 22 July 1804, when he described his scientific instruments in detail, he stated that the index error of the octant in the back observation was +2°11’40.3″; that is, it read high by that amount. Actually, the index error was +4°23’20.6″, but Lewis, when using the artificial horizon,[8]On land rarely is there a true horizon from which to measure the altitude of a celestial object. Lewis, therefore, had recourse to one of three artificial horizons they carried with them. One of them … Continue reading always divided the observed angle by two before subtracting the instrument’s index error, so 2°11’40.3″, as used, was correct. The problem, however, was that in 1805 Lewis used the wrong index error in his calculations. That problem began with his first observation, 12 April 1805, at the mouth of the Little Missouri River. There Lewis recorded the index error of the octant in the back observation to be +2°40’00” and he used this erroneous index error until September when he could again use the sextant to take the meridian observations. This simple mistake, by itself, makes all of Lewis’s latitude calculations, when using the octant, too far south by about 28’20”. To Lewis’s credit, he discovered this mistake while at Fort Clatsop during the winter of 1805–06 and recalculated some of the more important latitudes. Unfortunately, he either didn’t tell Clark about this error or Clark forgot about it, because Clark used the incorrect latitudes for all of his post-expeditionary maps.
Lewis’s meridian observation of the sun on the 21 August contains an obvious error. Although he recorded an angle of 69°15′ on the nineteenth, and 70°00′ on the twentieth, he recorded an angle of 72° on the twenty-first. Because the sun’s declination[9]For an observer on earth the declination of a celestial body is the angular distance of that body north or south of the plane of the equator as projected out into space to that celestial body. was decreasing by about 20′ per day, Lewis’s measured double angle should have increased by about 40′ per day; instead, it increased by 45′ between the 19th and the 20th and 2° 00′ between the twentieth and twenty-first. So, how did he derive a latitude of 44°30’21.7″ N from it? Likely, he actually read an angle of 70°32 or 70°42” from which he made his calculations, but later miscopied it as 72° to his journal.
The latitudes recalculated from Lewis’s three meridian observations of the sun taken at Fortunate Camp are: 44°57′ (19 August), 44°59′ (20 August) and 45°39′ (21 August). If his observation on the twenty-first actually was 70°32′ then the latitude becomes 44°55.5′, and if the angle was 70°42′ the latitude is 45°00.5′. Comparing these results with the latitude of 44°59’36” suggested for Fortunate Camp at the “forks of the Jefferson,” Lewis’s octant observations are right on the money.
Equal Altitudes
Lewis’s meridian altitude observations, for the most part, were exceptionally good despite his erroneous calculations. But what are we to make of the latitude from the “Hor  of the P.M. observation” of the sun’s center taken on 20 August? The only angle that Lewis gives for the equal altitudes observation for that date is 68°30′. This angle is the “double altitude” of the sun’s center above the horizon at 3:57:16 P.M. The altitude of the sun above the horizon calculated from that observation is derived as follows:
of the P.M. observation” of the sun’s center taken on 20 August? The only angle that Lewis gives for the equal altitudes observation for that date is 68°30′. This angle is the “double altitude” of the sun’s center above the horizon at 3:57:16 P.M. The altitude of the sun above the horizon calculated from that observation is derived as follows:
| Lewis’s observed double altitude | 68° 30′ 00″ |
| subtract the sextant’s index error | 00° 08′ 45″ |
| 68° 21′ 15″ | |
| divide by 2 | 34° 10′ 38″ |
| subtract (refraction + parallax)[10]The earth’s atmosphere bends a ray of light from a distant object unless that object is directly overhead; this bending of a light ray is called refraction. Refraction makes a body appear … Continue reading | 00° 01′ 01″ |
| sun’s center per Lewis’s observation | 34° 09′ 37″ |
By averaging the time of the AM and PM Equal Altitudes observation and correcting for the sun’s changing declination, the chronometer’s error on Local Time can be determined.[11]Lewis’s chronometer was of the type known as an Arnold’s watch; it was more like a large pocket watch than the typical chronometer pictured for use aboard ship. During the summer of 1805 … Continue reading From this, then, the true Local Time of the observation can be found, and by using the astronomical tables for August 1805, the sun’s altitude for this observation can be calculated. The calculation shows that the sun’s center should have been at 34°04’15” above the horizon, not 34°09’37”. This is a substantial difference and must indicate an error in the observation. Is this why Lewis calculated a latitude of 44°33’50.5″ N (27′ latitude or 30 miles too far south)? No, there must be some other problem, because making a calculation such as Lewis might have made with his own data yields a latitude considerably farther to the north.
Lewis’s Procedure
The following steps might be the way Lewis prepared his observational data to calculate the latitude from an Equal Altitudes observation.
- From the Equal Altitudes observation on the twentieth, determine the Chronometer’s error on Local Apparent Time; that is the time shown by the sun on a sun dial.
Using the times Lewis recorded in his journal for this observation, he should have found that the chronometer was 22 minutes 32.8 seconds too fast compared to Local Apparent Time. - Correct the time of his afternoon Equal Altitudes observation to true Local Apparent Time.
Note: if we can assume that Lewis actually made his calculation on the twentieth, then he probably did not apply the chronometer’s daily rate of loss because he would not have known it until after he calculated the chronometer’s error from his Equal Altitudes observation on the twenty-first.
Correcting the chronometer’s time by using the error it showed at noon on the twentieth should have yielded a time of 3:34:43 PM for the observation. - Find the difference from the time of Local Noon (12:00:00) and multiply it by 15: +3:34:43 x 15 = 53°40’45” = Local Hour Angle
- Correct the observed sextant altitude of the sun’s center for double altitude, index error, refraction and parallax.
This is how Lewis would have done it: Divide the double altitude 68°30′ by 2 = 34°15′; from 34°15′ subtract the sextant’s index error of 8’45” = 34°06’15”.
At this point Lewis would have made his first substantial error. Both he and Clark subtracted the sextant’s full index error after dividing the observed angle by two when using the artificial horizon. They either should have a) subtracted the full error before halving the observed angle or b) subtracted half the index error after halving the observed angle. This erroneous procedure makes all their observed altitudes too low by 4’22.5″ and latitudes too high by the same amount. Here Lewis should have derived an altitude of 34°10’37.5″, but this calculation will be made as Lewis would have done.
From 34°06’15” subtract the refraction of 1’08” found in his book of tables = 34°05’07”, finally add the parallax of 7″ from that book of tables = 34°05’14”. - From the Nautical Almanac determine the declination of the sun at the time of the observation: +12°23’31”.
It is possible that Lewis used the sun’s declination at noon Greenwich time instead of attempting to adjust it for his estimated longitude and observation time. The results of that possibility also will be shown.
At first one might suspect that Lewis’s error derives from the incorrect methodology (see Step 4, above) that he and Clark used when they made calculations from an observation employing both the sextant and the artificial horizon.
But Lewis’s calculation puts the latitude too far south, not north! Lewis doesn’t show his calculations or explain how he derived his result. He may have made an honest try at the calculation, but it’s possible that he was unable to work the mathematics and came up with a number that seemed to fit the results of his meridian altitude observations—and accepted that as a valid figure.
Latitude Errors
With the values: sun’s Local Hour Angle = 53°40’45”, altitude of sun’s center = 34°05’14” and sun’s declination = +12°23’31”, Lewis is ready to use spherical trigonometry (possibly from an example in Kelley’s Spherics) and solve the equations for his latitude. It’s a lengthy calculation, so only the results are shown here.
After Lewis has solved the spherical triangle using the above data, he should have derived a latitude of 45°04’45” N. But if Lewis had made his calculation after correctly figuring out the sun’s altitude (that is, using 34°09’37” instead of 34°05’14”) he should have obtained a latitude of 44°50’37″N. The camp was at 44°59’36” N. Lewis, however, obtained a latitude of 44°33’50.5″ N from this calculation. How?
Suppose Lewis made his calculation using the sun’s declination at noon Greenwich time +12° 32′ 40″ instead of adjusting it to his estimated longitude, but kept the values of 53°40’45” for the Local Hour Angle and his incorrect sun’s altitude of 34°05’14”. What latitude would he have obtained?
Solving the spherical triangle with these data gives a latitude of 45°26’05″N. Note, however, that for the step just previous he would have obtained a value of 44°33’55”; this is the camp’s co-latitude (90°—latitude). Did Lewis forget that he needed to subtract the co-latitude from 90° to get his latitude and, because 44°33’55” (or 44°33’50”) seemed to fit the values derived from his meridian altitude observations, he accepted that value? Or, because of his unfamiliarity with the calculations, did he make some other error that can’t be traced?
Other Problems
Part of Lewis’s error in latitude for this observation can be found in the times recorded for the Equal Altitudes observation. If you look carefully at the times recorded for the Equal Altitudes observations for the morning of the twentieth you will see that the time interval between the first and second observations is out of step with that between the second and third. You will also note that the average time of the observation is significantly greater than the time of the sun’s center. Similar errors exist in both the morning and afternoon observations for the twenty-first. In each case, the person who read the chronometer read it incorrectly by exactly one minute. Additionally, as noted above, if you calculate the altitude the sun should have been above the horizon at the corrected chronometer time, you find that either Lewis misread the sextant or mis-recorded the angle, or that the chronometer was running erratically.
Jefferson’s “Failure”
Before the expedition got underway, Thomas Jefferson expressed the need to have all of the expedition’s celestial observations recalculated by competent mathematicians after the expedition’s safe return. However, he failed to make certain, while he was still president, that this necessary operation was done. The reasons for this “failure” belong to another part of the expedition’s story. But suppose those re-calculations had been made. For example, Lewis didn’t attempt to calculate the latitude from the Equal Altitudes observation of the twenty-first, but that observation could have provided a check on the latitude of Fortunate Camp, as well as upon Lewis’s other calculations. What would that observation have shown?
For the observation on 12 August 1805, (a) determine the altitude of the sun’s center correctly, 32°53’19”; (b) adjust the chronometer’s time of the observation to reflect the chronometer’s daily rate of loss, 3:40:40 PM; and (c) approximate the longitude of the observation from Clark’s maps and factor in the time of observation to obtain a value for the sun’s declination more nearly what it should have been, +12°03’29”.
Using the above values produces a latitude of 44°55’42”. This comes very close to the average recalculated latitudes from Lewis’s meridian altitude observations, and less than 4′ latitude (5 miles) south of the latitude of 44°59’36” for Fortunate Camp arrived at from the expedition’s survey data and journal descriptions.
Longitude
Despite the advancements in chronometer technology since John Harrison constructed a time piece in the mid-1700s that met the specifications of Great Britain’s Commissioners of Longitude, finding a longitude on sea or on land was still a difficult process in 1805. The usual limits of accuracy often were as great as ± 15 minutes; at 45° north latitude, an error of 15′ of longitude means an error of ± 12 miles.
Lewis took a series of observations on 19 August, and another series on the twentieth, to obtain the data necessary to calculate a longitude for Fortunate Camp. However, he did not make any calculations from them.[12]Jefferson directed Lewis to take the necessary observations for the determination of longitude, but did not expect him to make the complicated calculations. These were to be made by mathematicians in … Continue reading How good were his observations?
Long-time practical navigator Bruce Stark of Eugene, Oregon, suggests that Lewis missed the longitude for Fortunate Camp by a mere three miles.[13]Letter to the Editor, We Proceeded On, Vol. 28, No. 3 (August 2002), 3-4. Such an observation was far better than what most trained navigators could do at that time and as good as, and even better than, the average longitude values determined by the great Canadian trapper-surveyor David Thompson. My method of checking Lewis’s observations for longitude is somewhat different from that used by Mr. Stark. From a software program I determine the apparent positions of the celestial objects, then back-calculate to the angle Lewis should have observed for the time and his location. From these calculations I conclude that the angular error of Lewis’s observation on the nineteenth was 13 arc seconds too small and on the twentieth it was 38 arc seconds too large. Given the rate at which the sun and moon were approaching each other at the time those observations were made, my findings are in complete agreement with those calculated in the standard method by Mr. Stark.
Dimensions of Navigation
The foregoing discussion summarizes the mathematical dimension of celestial navigation on land; an orderly sequence of measurements, addition, subtraction, multiplication, division. The second dimension of the process is physical. The technique of making a meridian observation of the sun with an octant by the back sight method, on land, using an artificial horizon is a difficult operation. The observer does not stand bold upright looking toward the horizon as the common image of the marine navigator depicts, but must hold the handle-less instrument in the left hand, usually while kneeling down or sitting cross-legged, looking down at a very steep angle into the artificial horizon while trying to adjust the index arm with the right hand until the image from the index mirror and that reflected from the artificial horizon (there was no telescope on Lewis’s octant) were matched. It was not much easier using the sextant and artificial horizon except that you could hold the instrument in your right hand. And then there were the observations taken at night by torchlight with mosquitoes, flies, gnats and fatigue that could strain the last fiber of an explorer’s soul. Despite these ordeals, the captains made these observations at nearly every significant point along the route.
The third dimension might be called the contextual setting. The moments devoted to celestial observations were islands of intense concentration and mental exertion injected into the dense daily array of routines, opportunities, anxieties, and unforeseen occurrences. In that context, especially during the busy fortnight at Fortunate Camp, it is remarkable that their observations provided coordinates that were as close to correct as they were. Bearing this in mind, it is easy to forgive the captains the few errors they committed.
An Extra Dimension
For the Corps of Discovery there was yet one more dimension to the carrying out of celestial observations. Consider the baffled Indian onlookers, wondering what occult rituals the white chief and his acolytes were practicing. Was sign-talker George Drouillard equal to this challenge? Could his eloquent hands, which so often had bridged cultural chasms to shape mutual understandings, reduce this arcane tale to concepts that could be grasped? How could he possibly have explained the sextant and octant, when the magic of the compass needle was simply “medicine” to Indian people? How could he have expressed their uses and purposes to people without words of their own for hour, minute, degree, arc, second, angle, decimal point, or statute mile? Never mind all that, and the murky labyrinths of trigonometry and spherical geometry through which even the captains took wrong turns. How might Drouillard have broached the bold preposterous concept of Earth as a globe to people with their own holy mysteries of sun, moon, stars, land, and sky, who already had orderly, practical understandings of time, space, pace and place? Or would a mere nod, a smile, and a shrug have satisfied their inquisitive eyes?
Notes
| ↑1 | The “No. 43” stands for “Point of Celestial Observation Number 43,” their forty-third such point of observation since leaving Fort Mandan. |
|---|---|
| ↑2 | On the earth a meridian is any line that passes through the north and south poles and is perpendicular to the equator. The half of the meridian circle that is on the observer’s side of the globe is called the upper meridian. A meridian altitude is a celestial observation taken when the object observed (usually the sun) is on the observer’s upper meridian and thus at the highest point that it reaches above the plane of the equator that day. |
| ↑3 | Lewis’s sextant was in the form of an arc encompassing one-sixth of a circle, hence the name sextant. Because a sextant uses an index mirror to reflect objects to a second mirror and then into the eyepiece, the angles (degrees) marked on its graduated arc are double the actual. That is, a sextant actually could measure an angle of 120°, but this compresses the angle (degree) marked on the graduated arc very close together even though the radius of that arc on Lewis’s sextant was ten inches. Each of the degree marks, in turn, was equally divided into four parts of 15′ each. The instrument also had a vernier (Lewis called it a nonius), which allowed him to interpolate the angle to 15″. Finally, there was a micrometer screw that allowed him a further interpolation down to 7-1/2″. To read this angle, even with the attached magnifying glass (Lewis called it a microscope) was no easy task, especially when it had to be done in a short time and under difficult conditions. Errors sometimes did occur. Like all precise scientific instruments, a sextant could become out of adjustment, especially when it had been banged about on a storm-tossed ship or in a canoe on the Missouri or Jefferson River. Lewis recorded that his sextant had an index error of 8′ 45″. What he actually meant was that the sextant read too high by 8′ 45″ and, to correct for this error the person doing the calculations had to subtract 8′ 45″ from the angle measured. Usually an instrument’s index error is corrected before any other calculations are made. A vernier is a scale for measuring smaller subdivisions of a scale or circle than can be done by estimation; Lewis called this device a nonius, but that term is obsolete now. On a sextant or octant the vernier measures an of arc of about 20° and is so graduated as to have one line less (or more) than the equivalent distance or angle on the main scale or arc. Lewis said that with the vernier he could read his sextant to 15 seconds (15″) of arc. Therefore, its vernier contained 60 equally spaced lines that encompassed an arc of 14° 45′ or (less likely) 15° 15′; that is, 60 lines on the vernier spanned the same arc as 59 (or 61) spaces of 15′ each on the main scale. The 60 lines on the vernier were blocked into groups of four. The first line was marked with a symbol to indicate the 0 mark or starting point. The 20th, 40th and 60th lines were marked 5, 10 and 15, respectively. |
| ↑4 | The octant also was a device to measure the angle between two objects. Although its graduated arc spanned 45° (an eighth of a circle, hence octant) it could measure an angle of 90° (when used in the fore sight method) because it utilized the principle of reflection of a ray of light from two mirrors. Lewis’s octant, with a radius of 14 inches, was fitted with an additional peep sight and mirror on the “back” limb. Using the octant in the “back sight method” Lewis, with the help of geometric principles, could thus “measure” an angle of 180°. |
| ↑5 | It appears that Lewis uses the abbreviation “Hor” to mean “horizon.” Combining it with the geometric symbol for angle creates the expression “horizon angle.” It refers to the altitude of the sun above the horizon at the time of the PM observation for Equal Altitudes. |
| ↑6 | An equal altitudes observation is a two-part process. The first set of measurements is taken when a celestial object is east of the observer’s meridian and the second set is taken when the object is west of the observer’s meridian. The equal altitudes observation provides information from which calculate several types of navigational information may be calculated. Lewis and Clark, however, used the observation exclusively to check the time of their chronometer. |
| ↑7 | The index error (sometimes called instrument error) is the angular difference between what the instrument measures and what it actually should measure if it were in perfect alignment. The error usually occurs because the mirrors get slightly out of adjustment when the instrument is handled or mishandled. Most navigators merely determine the index error on a regular basis and factor that error into their calculations rather than taking the time and trouble to adjust the mirrors for every use. |
| ↑8 | On land rarely is there a true horizon from which to measure the altitude of a celestial object. Lewis, therefore, had recourse to one of three artificial horizons they carried with them. One of them was simply a tray filled with water and protected by a wind screen. The other two used mirrors as reflecting surfaces, but the mirrors had to be leveled with extreme care. |
| ↑9 | For an observer on earth the declination of a celestial body is the angular distance of that body north or south of the plane of the equator as projected out into space to that celestial body. |
| ↑10 | The earth’s atmosphere bends a ray of light from a distant object unless that object is directly overhead; this bending of a light ray is called refraction. Refraction makes a body appear higher above the horizon than it actually is, and its effect must be removed from the observed altitude of a celestial body to derive a correct latitude. Finding the amount that must be subtracted is done either by consulting special tables, or by using an appropriate formula. The expedition carried Nevil Maskelyn’s Tables Requisite to be Used with the Nautical Ephemeris for Finding the Latitude and Longitude at Sea (London, 1781), and Patrick Kelly’s Nautical Almanac and Astronomical Ephemeris . . . (London 1781-1804). Parallax, for a heavenly body, is the angular difference between the altitude of that body as an observer would see it if there were no refraction, and the body’s altitude “seen” from the center of the earth at the same time. Parallax always makes a celestial body appear lower in the sky than it actually is. Lewis could find the value to be added for parallax from the Tables Requisite referenced above. In the example from Lewis’s Equal Altitudes observation on the 20th, parallax (+7″) was combined with refraction (-1′ 08″). |
| ↑11 | Lewis’s chronometer was of the type known as an Arnold’s watch; it was more like a large pocket watch than the typical chronometer pictured for use aboard ship. During the summer of 1805 Lewis’s chronometer usually lost about 30 seconds per day. On the 20th the chronometer was 19 minutes 29.4 seconds fast, and this value can be verified by the altitude of the sun’s center during the afternoon equal altitudes observation. On the 21st, however, the equal altitudes observation appears to show that the chronometer was only 18 minutes 33.6 seconds fast, a loss of 55.8 seconds per day. This suggests that either the observation for the 21st either contains an error, or the chronometer was beginning to run erratically again. |
| ↑12 | Jefferson directed Lewis to take the necessary observations for the determination of longitude, but did not expect him to make the complicated calculations. These were to be made by mathematicians in the War Department. The expedition’s data ultimately were delivered to Ferdinand Hassler, a Swiss mathematician of the faculty of the newly founded (1802) U.S. Military Academy at West Point, but for various reasons the task never was completed. Moulton, Journals 2:533-34. Richard S. Preston, “The Accuracy of the Astronomical Observations of Lewis and Clark,” Proceedings of the American Philosophical Society, vol. 144, no. 2 (June 2000), 169–91. |
| ↑13 | Letter to the Editor, We Proceeded On, Vol. 28, No. 3 (August 2002), 3-4. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.