Point of Observation No. 51, 2 November 1804 through 17 April 1805
A late winter snow squall has dusted the leafless cottonwood trees and the dormant grainfields. The triangular structure at photo center is a replica of Fort Mandan built by local volunteers in 1972. It is two miles via good roads from the Lewis and Clark Visitor Center at Washburn, North Dakota. The original site of the fort, where no remains have ever been found, was about fifteen miles up the Missouri from here, closer to the mouth of the Knife River. Access to it is discouraged.
The two ranks of cottonwood trees, which take root a short distance from water, mark the shifting of the river’s course over a period of many years. Annually, those snow-covered sand bars are submerged by the spring freshet. When the high water recedes, they will have been moved and reshaped by the river’s current. The Corps of Discovery often used the ice-covered river as a travel route, but the Missouri has not frozen solid in this vicinity within the past fifty years, mostly because the dams upstream—chiefly Garrison Dam, 35 miles away, and Fort Peck Dam 382 miles above that—have changed the temperature and velocity of the river’s current.
—Joseph Mussulman and Robert Bergantino
During the final weeks of October 1804, the Lewis and Clark Expedition awoke to temperatures near or below the freezing point. Blustery northern winds brought icy rain and snow. V-formations of honking geese filled the skies daily, winging their way south to escape the rigors of the northern winter. Meanwhile, contrary to the flow of the river and the advance of the cold, the Expedition pushed northward. On 27 October 1804, after having traveled more than 1200 river miles from the mouth of Kansas River by their estimate, the Corps arrived at the Mandan–Hidatsa villages near the mouth of Knife River (near present-day Stanton, North Dakota). William Clark spent part of the next few days seeking a suitable site for the Expedition’s winter quarters. He chose a location a few miles downstream from the villages but on the east side of the Missouri. By 2 November 1804, with construction just getting underway, the captains named the encampment Fort Mandan in honor of their Mandan neighbors.
Key Location
In the early 1800s, the agglomeration of Mandan-Minitari villages was the most important trade and population center between the Mississippi River and the Cascade Mountains north of Santa Fe. Not even St. Louis could boast having so many citizens nor such an exchange of goods. The Mandans, a Siouxan-speaking Nation, once lived near Lake Michigan, possibly in southern Wisconsin or northern Illinois before moving westward to the Missouri. After reaching the Missouri they had moved their villages many times—always farther up the Missouri River. The Mandans and the Minitari (also Siouxan-speaking, but distantly related) eventually gathered their villages near each other for mutual protection against another linguistically related nation, the Dakota or Sioux proper. The western Dakota also were an important trading nation, but because of their numerical superiority and their alliances, they were able to influence or control trade coming up the Missouri. The Mandan and Minitari, consequently, traded almost exclusively with the British-Canadian posts. In 1804, however, these villages were within the area comprising the Louisiana Purchase. Meriwether Lewis thought that trade with these nations now should belong to traders from the United States. The British-Canadians saw it differently. Not only that, the natural boundary (not geographically well defined) between Louisiana and British claims lay only a score of miles or so northeast of the villages. Who was going to stop them from such a lucrative trade?
In December 1797, the Canadian trader-surveyor-mapper David Thompson had stopped at the Mandan villages. In January 1798, Thompson took celestial observations at the villages and determined them to be at a latitude of 47°17’22″N and a longitude of 101°14’24″W. Why then did Lewis and Clark think it necessary to take twenty-six observations during the bitter cold winter that dragged on until late March? Lewis’s persistent Anglophobia may have had much to do with the many celestial observations he took. He may have suspected that Thompson’s coordinates had been altered for political purposes before they reached Jefferson. On the other hand, Lewis may just have wanted to see if he could verify the site’s location with independent data of his own taking. At any rate, the location of these villages was as important as any river junction or mountain pass. Cold weather or no, the observations had to be taken!
Chronology
| Date | Source | Coordinates |
|---|---|---|
| 1797 | Atlas Map 5[1]Maps numbers are those given in Moulton, Journals, Vol. 1. | 48˚N, 110˚W, approximately, villages |
| Evans ca. 1797 | Atlas Map 12 | “This meridian[2]The meridian identified passes through the Mandan village. is 7˚23′ west longitude from Ft. Charles or17˚33′ west of St. Louis[3]St. Louis is at about 90°10′ west, thus the Evans map would place the Mandan village at about 107°43′ W. calculated from the parallel of the middle[?] latitude.” Latitude by observation 47˚42’35" [4]This line is shown several miles south of the Mandan village. Variation of the compass 1 point N.E.[5]That is, 11¼° East. |
| 1798 Jan 10 | Thompson, D | 47˚17’22", 101˚14’24"[6]From Thompson’s celestial observations. |
| 1803, King | Atlas Map 2 | 47˚25’N, 101˚05’W[7]These coordinates for the Mandan village are approximate and likely are from David Thompson’s celestial observations. |
| 1805, Clark | Atlas Map 32a | 47˚31’N, 101˚08’W, Fort Mandan (State Department copy) |
| 1805, Clark | Atlas Map 32b | 47˚32’N, 101˚02’W, Fort Mandan (War Department copy) |
| 1805, Clark | Atlas Map 32c | 47˚33’N, 101˚02’W, Fort Mandan (Hague copy) |
| 1805 | Atlas Map 33 | 47˚21’47", no longitude recorded, Fort Mandan |
| 1805 | Atlas Map 46 | 47˚21’47", no longitude recorded, Fort Mandan |
| 1806, L&C | Atlas Map 123 | 47˚28’N, 100˚48"W, Fort Mandan |
| 1810, Clark | Atlas Map 125 | 47˚15’N, 100˚57"W, Fort Mandan |
| 1814, L&C | Atlas Map 126 | 47˚22’30"N, 100˚57’30"W, Fort Mandan |
| May 1997 | Bergantino[8]The coordinates of this encampment were determined by “best-fit”-matching the Expedition’s latitudes and river survey to a detailed map by G.K. Warren (1856), a map by the Missouri … Continue reading | 47˚16’52"N, 101˚16’44"W Ft Mandan (1927 N. American Horizontal Datum) |
Schedule
| 1804 | |
| Dec | |
| 22 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 22 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| 1805 | |
| Jan | |
| 07 Lunar Distance from the Sun | (6 sets of the sun-moon distance and time) |
| 07 Lunar Distance from the Sun | (6 sets of the sun-moon distance and time) |
| 13 Meridian altitude of the Sun | (altitude of the sun at noon for latitude) |
| 14 Eclipse of the Moon for Longitude | (observation of eclipse elements sextant’s telescope and time) |
| 15 Eclipse of the Moon for Longitude | (observation of eclipse elements sextant’s telescope and time) |
| 15 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 15 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| 26 Meridian altitude of the Sun | (altitude of the sun at noon for latitude) |
| 28 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 28 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| Feb | |
| 06 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 06 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| 06 Lunar Distance from the Sun | (12 sets of observations of sun-moon distance and time) |
| 23 Lunar Distance from the Sun | (12 sets of observations of sun-moon distance and time) |
| 23 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 23 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| Mar | |
| 25 Magnetic Declination with Sun | (3 sets of the sun’s altitude and bearing + the time) |
| 28 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 28 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| 30 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 30 Equal Altitudes of the Sun PM | (3 observations of the sun’s altitude + the time) |
| Apr | |
| 03 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 03 Equal Altitudes of the Sun AM | (3 observations of the sun’s altitude + the time) |
| 03 Lunar Distance from the Sun | (7 sets of observations of sun-moon distance and time) |
Latitude
Lewis took meridian altitude observations on 11 November 1804, 13 January 1805 and 26 January 1805 (as he calculated them). The latitudes he calculated differed from each other by less than 1 arc minute; their average was 47°21‘ 24“. Although this average was about 4‘ north of that which Thompson obtained (47°17‘ 22“), Lewis must have felt his observations were satisfactory.
Lewis, however, did not realize that both he and Clark persistently made a mistake in their calculations from all observations obtained with both the sextant and the artificial horizon. The proper procedure was to subtract the sextant’s index error (usually 8‘ 45“) from the observed angle, then divide the result by two, because using the artificial horizon doubled the observed angle. Lewis and Clark, unfortunately, first divided the observed angle by 2, then subtracted the sextant’s index error. This meant that their calculations produced altitudes that were too low by an average of 4‘22½“, and thus made their calculated latitudes too far north by that same amount.
Lewis’s observations, calculated correctly, yield an average latitude of 47°16‘ 54“ N, not 47°21‘ 24“. The latitude for Fort Mandan usually given in the Journals is 47°21‘ 47““ ; this was for the observation made on 26 January 1805. Lewis must have thought that the observation on this date was more reliable than the others.
| Date | Lewis | Recalculated | Per Map Eval. | Thompson 1798 |
|---|---|---|---|---|
| 11 November 1804 | 47˚21′ 33" N | 47˚17′ 02" N | ||
| 13 January 1805 | 47˚20′ 53" N | 47˚16′ 22" N | ||
| 26 January 1805 | 47˚21′ 47" N | 47˚17′ 16" N | ||
| Average | 47˚21′ 24" N | 47˚16′ 54" N | 47˚16′ 55" N | 47˚17′ 22" N |
Local Apparent Time
The many Equal Altitude observations that Lewis made while at Fort Mandan leave little doubt that he was concerned about his chronometer—and with good reason. The chronometer had stopped twice without apparent cause since leaving Camp Dubois (and twice before that), and one other time it had been allowed to run down. The Equal Altitude observations were the key to regulating the chronometer and determining its error on Local Time.
Observations for the meridian altitude of the sun and double altitudes of the sun for latitude and calculations for latitude from them could be made without knowing the precise Local Time. To make calculations for latitude by the sun’s hour angle or calculations for longitude and magnetic declination, however, depended upon knowing the correct Local Time.
During the summer and early fall months of 1804, the chronometer’s daily rate of loss had averaged about 28 seconds. The winter cold, however, must have made the lubricating oil in the chronometer more viscous, increasing its daily rate of loss. In the seventeen days between the observations on 20 January 1805 and 6 February 1805, for example, the chronometer’s loss on Mean Time was 12 minutes 35.7 seconds; a loss of 44.45 seconds per day.
Although no mention is made of it in the journals, the chronometer must have stopped again between 6 February and 23 February 1806. At noon on the 6 February the chronometer was 1 hour 18 minutes 18.3 seconds slow on Mean Time, but at noon on the 23rd it was 2 hours 28 minutes 11.1 seconds slow on Mean Time. This difference of 1 hour 9 minutes 52.8 seconds (4 minutes 8.6 seconds per day) certainly is more than can be attributed to daily loss.
Some time between 23 February 1805 and the observation for Magnetic Declination on 25 March 1805 (again with no reference in the journals) the chronometer must have been reset either intentionally or accidentally, because it was 27 minutes 23.6 seconds fast on Local Mean Time. Later observations show that it continued to lose time, and was 24 minutes 26.3 seconds fast on 13 April 1805, four days before the Expedition departed Fort Mandan.
The Equal Altitudes observation of the sun provided Lewis a means to check the time shown by his chronometer. Using his sextant and an artificial horizon (usually a tray filled with water), Lewis would measure the altitude of the sun in the morning, and the times of these measurements, as shown by the chronometer, were recorded. In the afternoon, when the sun was at the same altitude it had been for the morning observations, Lewis would again measure its altitude, noting the times shown by the chronometer. These data, after allowing for the sun’s changing declination, would tell him what time the chronometer would have shown at noon. From another Equal Altitudes observation made the next day or some days later, Lewis could determine his chronometer’s daily rate of loss.
These Equal Altitude observations, made during the winter especially when the temperature was well below freezing, presented a special problem for Lewis. He preferred to use water as a reflecting surface (artificial horizon), but unless he used warm water and made his observations very quickly, the water would freeze. On several occasions at Fort Mandan, therefore, he was obliged to use a mirror leveled with a spirit level for these observations, and he did not trust that he could make the surface perfectly horizontal as a water surface would be.
Despite the problems with the chronometer, because Lewis took so many (nine) observations of Equal Altitudes of the sun while at Fort Mandan, his observations for magnetic declination and most of his observations for longitude can be calculated and made to yield useful results.
| Date | Apparent Time | Mean Time | Interval | Loss per Day |
|---|---|---|---|---|
| 1804 Dec 22 | 0:40:36.5 slow | 0:39:43.4 slow | — | — |
| 1805 Jan 15 | 0:52:01.8 slow | 1:01:57.3 slow | 24 days | 55.58 seconds |
| 1805 Jan 20 | 0:54:11.4 slow | 1:05:42.6 slow | 5 days | 45.06 seconds |
| 1805 Jan 28 | 0:57:48.6 slow | 1:11:13.8 slow | 8 days | 41.40 seconds (observation error?) |
| 1805 Feb 6 | 1:03:50.0 slow | 1:18:18.3 slow | 9 days | 47.17 seconds |
| 1805 Feb 23 | 2:14:29.2 slow | 2:28:11.1 slow | — | — |
| 1805 Mar 28 | 0:32:45.0 fast | 0:27:34.6 fast | — | (observation error?) |
| 1805 Mar 30 | 0:31:33.3 fast | 0:26:58.9 fast | 2 days | 17.85 seconds (?) |
| 1805 Apr 3 | 0:27:47.6 fast | 0:24:26.3 fast | 4 days | 38.15 seconds |
Latitude from Lunar Eclipse
Before the Expedition left its winter quarters at Camp Dubois in May 1804, Lewis had obtained some of the more reliable maps and data available concerning Western geography. The most important geographical information regarding the location of the Mandan village came from the celestial observations David Thompson took on 10 January 1798. Lewis had received these coordinates from Thomas Jefferson and may not have known who took the celestial observation or how reliable they might be (the trading companies tried to keep Thompson’s maps and data for themselves). Lewis knew that Jefferson had obtained the coordinates from a British source, and Lewis may have had reason to suspect that the coordinates had been altered before coming into Jefferson’s hands. Whether this is the case or not, Lewis certainly wanted to have data of his own taking to compare in order to verify or refute these other coordinates.
In the early 1800s there were several means of obtaining one’s longitude—all involved comparing the correct time at your location with that at Greenwich. Before telegraphy this required using a chronometer or reliable watch to obtain the time for a celestial event and comparing that time to the Greenwich time for that event as given in the Nautical Almanac. Some of the more common celestial events whose times could be used were: an eclipse of the moon; immersions or emersions of Jupiter’s satellites; occultations of stars or asteroids by the moon; and distance of the moon from the sun or one of eight or ten stars (Lunar Distance Observation). Most of these methods worked better in theory than in application to persons untrained or inadequately trained in taking the observations or making the calculations.
Lewis’s mainstay observation for longitude was the Lunar Distance Observation, though here at Fort Mandan a fortuitous eclipse of the moon presented him with another opportunity, and this observation would have given him his best longitude—if he had calculated it correctly.
The 1805 Nautical Almanac noted that a total eclipse of moon would begin on 14 January 1805 at 18:42 hours Greenwich Apparent Time. Astronomers at that time, however, began their day at noon, so 18:42 hours meant, not 6:42 pm as it would today, but 6:42 in the morning. Using Thompson’s longitude of 101°14’24” West would place Fort Mandan about 6h 45m earlier than Greenwich. This meant that the eclipse would begin about midnight local time 14-15 January. Lewis, however, was not sure he could trust Thompson’s longitude, and this necessitated his going outside to start his observations perhaps as much as an hour before time so as not to miss the beginning of the eclipse.
The temperature was bitterly cold. The high temperature for 14 January was about 8° below zero and the temperature was 10° below zero at sunrise on the 15th. Lewis had nothing more than the telescopic eyepiece from his sextant to observe the eclipse, and the chronometer to time it. The sky was partly to mostly cloudy, and Lewis was unable to see the beginning of the eclipse. He was, however, able to time four of the five principal elements of the eclipse: 1) the commencement of total darkness, 2) the middle of the eclipse, 3) the end of total darkness, and 4) the end of the eclipse. Now all he had to do is obtain the correct time from his wayward chronometer.
Lewis had taken an Equal Altitudes observation of the sun on 22 December 1804 and had calculated that his chronometer was 39m 37.6s slow on local mean time (I calculate 39m 43.4s). He, however, needed another Equal Altitudes observation as soon after the eclipse as possible to find the chronometer’s error then and, from it, the chronometer’s daily rate of loss. Lewis took an Equal Altitudes observation on the 15th but he was unsatisfied with it because, 1) owing to the cold, he had to use a leveled mirror as an artificial horizon and 2) clouds moved in during the afternoon and interfered with two of the three measurements he had to take.
Lewis made another Equal Altitudes observation on 20 January 1805 and calculated that the chronometer was 1hr 15min 20.3sec slow on Local Mean Time. Lewis, however, must have thought that this observation also was unsatisfactory for he did not use the times from it to calculate the longitude from the eclipse. Fortunately he didn’t use the chronometer error he derived from that observation because he had miscalculated the chronometer error. The chronometer’s actual error on Local Mean Time 1hr 05m 43.6s slow, not 1hr 15m 20.3 s slow. If Lewis had calculated the chronometer error correctly for this observation he could have continued with his eclipse calculations because the observation actually was reliable.
Lewis, on 28 January 1805, made yet another Equal Altitudes observation. From this observation he calculated that his chronometer was 1hr 11m 12.2s slow on Local Mean Time (I get 1 hr 11m 18.8s slow). Using this latest Equal Altitudes observation and that for 22 December 1804, Lewis calculated his chronometer’s daily rate of loss and from that determined how slow his chronometer would have been on Local Mean Time during the eclipse. Comparing the corrected Mean Time for the end of total darkness and that the end of the eclipse with the times given in the Nautical Almanac he derived a longitude of 99°22’45.3″ from the time for the end of total darkness and 99°26’45” from the time for the end of the eclipse. The average of these two longitudes, however, puts Fort Mandan at 99°24’45” West or too far east by 1°52′! Where did Lewis go wrong?[9]The main reason the longitude Lewis derived was so far east of the actual longitude is that he made his time comparisons with those given in the Nautical Almanac using his calculated Local Mean … Continue reading [10]Lewis also made a mistake in how he determined his chronometer’s error. He might have discovered this if he had recalculated the times of his observations and made a plot (graph) of the … Continue reading
Longitude from Lunar Distances
While at Fort Mandan, Lewis made observations of the Lunar distance from the sun for longitude on four different dates. He recorded making only one attempt to calculate a longitude from them; this was on 23 February 1805. On that date Lewis completed the Lunar distance observation less than ten minutes before he began his Equal Altitudes observation to check his chronometer. From this Equal Altitudes observation he calculated that his chronometer was 2 hr 14 min 25.7 sec slow on Local Apparent Time at noon (using modern data I calculate 2:14:29.2 slow). He, however, had taken no Equal Altitude observations since 6 February to check the chronometer’s daily rate of loss, but must have felt he could make a valid correction. Let’s look at his efforts:
| Time (A.M.) h m s |
Distance ˚ ‘ " |
Time h m s |
Distance ˚ ‘ " |
|---|---|---|---|
| 6 12 15 | 66 24 15 | 6 25 56 | 66 20 00 |
| 6 14 17 | 66 23 43[11]This should be 66°23’45” as sextant can be read only to the nearest 1/8 minute (7½ seconds). | 6 28 05 | 66 19 15 |
| 6 16 14 | 66 22 45 | 6 29 06 | 66 19 00 |
| 6 17 51 | 66 22 00 | 6 30 58 | 66 18 00 |
| 6 20 23 | 66 21 25[12]This should be 66°21’22.5″ as sextant can be read only to the nearest 1/8 minute (7½ seconds). | 6 32 38 | 66 17 45 |
| 6 22 18 | 66 21 00 | 6 34 59 | 66 17 15 |
| Lewis | Re-calculated | |
|---|---|---|
| Latitude of place of observation | 47˚21’47" | 47˚16’52" |
| [Average] Time by chronometer of observation | 6h 23m 45.0s | 6h 23m 45.0s |
| Chronometer too slow apparent time at noon | 2h 14m 25.7s | 2h 14m 29.2s |
| True time of observation as shown by the chronometer | 8h 38m 10.7s | 8h 38m 03s |
| True apparent time of observation A.M. as deduced from mean time by the application of the equation of time with its sign changed | 8h 38m 18s | 8h 38m 07s |
Distance of  ‘s and ‘s and 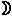 ‘s nearest limbs at the time of this observation, ‘s nearest limbs at the time of this observation, |
66˚ 20′ 31.7"[13]This angular distance includes the sextant’s index error of 8’45”, which must be subtracted. Additionally, the sun’s semidiameter and moon’s semidiameter plus its … Continue reading | 66˚ 20′ 31.9" |
| Estimated Greenwich time of observation | 15h 15m 57.7s[14]To obtain this time, Lewis would be using a longitude of 99°24’55.5″ west though probably it was 99°25′, a rounded average of the two values he obtained from his observation … Continue reading | 15h 23m 07 |
| 9˚ 52′ 06.8"s[15]At 15h15m57.7s Greenwich Apparent time the sun’s declination should have been -9°49’15.9″. The sun’s declination was 9°52’10” south at Greenwich Apparent … Continue reading | 9˚49 ‘03.6"s | |
| True mean time of observation at this place A.M. | 8h 51m 59.5s | 8h 51m 50.2s |
| Hour ∠ of the A.M. observation | 50˚ 25′ 03"[16]Hour angle (or HA) = sun’s hour angle. The sun’s forenoon Hour Angle = [(12h—Apparent AM Time of observation) x 15]. Lewis, however, should have calculated 50°25’30” … Continue reading | 50˚28′ 15" |
Altitude of the  ‘s center at time of observation by Mr Ellicott’s formula ‘s center at time of observation by Mr Ellicott’s formula |
17˚ 24′ 00" | 17˚24′ 20" |
By Mr Patterson’s Altitude  ‘s center at time of observation ‘s center at time of observation |
18˚ 30′ 56."[17]The fault for the difference between the sun’s altitude that Lewis derived from Ellicott’s formula and Patterson’s lies in Robert Patterson‘s Astronomy Notebook that Lewis … Continue reading | 17˚24′ 19" |
What longitude might Lewis have calculated from this observation? That longitude would depend upon 1) the method he used for “clearing the lunar,” 2) how he interpolated the logarithms he needed to use and, of course, 3) the accuracy of his mathematics.
Robert Patterson provided Lewis with a method of clearing the lunar. Ellicott also must have given Lewis a method to use, and there were other methods including that by Nathaniel Bowditch. The method that was considered the most rigorous was that by Chevalier Jean Borda in 1787. Methods for clearing the lunar continued to be developed every few years up to about 1920 when the lunars became obsolete except for a steadfast handful of navigators who still practice (and improve upon) the method today.
Taking a Lunar Distance required practice, steady hands and good eyesight. Using the sextant, an observer sighted the sun, moon or star through the sextant’s horizon glass. After finding the other body (sun or moon) in the index mirror, the two objects were optically brought together until they just touched. The observer called “Time,” and the time shown by the chronometer was noted while the observer read the angle measured by the sextant. This operation was repeated until (usually) six to eight measurements had been obtained, often over a period of twenty minutes to one-half hour.
For the observation of 23 February 1805 the sun and moon were at 17.5° and 14.3° above the horizon, respectively. This meant that the sextant had to be held nearly horizontal to make the observation. The observer usually tried to keep the “working side” of the sextant upwards, but for some moon-star observations it was necessary to turn the “working side” downwards. Sextant positions or attitudes had much to do with the accuracy of the observation because of fatigue. Reading the angle measured on the index arm also could be difficult, especially at night using torchlight.
If accurate and reliable observations for Lunar Distance were difficult to take, making the calculations that converted the observed data into longitude was equally challenging—and much more time-consuming.
Preliminary Calculations
Step 1: The times and distances from the observation should be plotted to evaluate them and reject data pairs that look spurious,
Step 2: Using the valid data pairs, averages for the time and for the distance are calculated,
Step 3: The true Local Mean Time must be determined from the chronometer time—usually from data obtained by Equal Altitudes observations before and after the Lunar Distance observation,
Step 4: Convert Local Mean Time of the observation to Local Apparent Time using the Equation of Time ratioed to your estimated or dead-reckoned longitude,
Step 5: From the Local Apparent Time, calculate the sun’s hour angle (15 x the number of hours before or since Local Apparent Noon),
Step 6: Using data from the Nautical Almanac find, for the moon and the sun or star its 1) Right Ascension, 2) Declination, 3) semidiameter (sun and moon only) and 4) moon’s horizontal parallax. All these parameters must be adjusted (ratioed) to the time of the observation using the estimated longitude,
Step 7: Using the proper formula together with a book of trigonometric logarithms, calculate the altitude of the sun’s center from its hour angle and declination and the known latitude,
Step 8: Using Tables Requisite find the refraction and parallax for the true altitude determined and calculate what the apparent altitude the sun would have been for this observation.
Step 9: From the sun’s right ascension at the time of the observation, the time of the observation and the moon’s right ascension, calculate the moon’s hour angle,
Step 10: Using the proper formula together with a book of trigonometric logarithms, calculate the altitude of the moon’s center from its hour angle and declination and the known latitude
Step 11: Using Tables Requisite find the refraction and parallax for the true altitude determined and calculate what the apparent altitude the moon would have been for this observation (if the Lunar distance observation was between the moon and a star, steps 8, 9 and 10 must be repeated),
Step 12: From Tables Requisite and the altitude for the moon obtained in step 10, find the moon’s augmentation,
Step 13: From the average lunar distance, subtract the sextant’s index error,
Step 14: If the observation was between the sun and moon, to the result of Step 13 add the sun’s semidiameter and the moon’s semidiameter plus augmentation. If the observation was between the moon’s near limb and a star, add just the moon’s semidiameter and augmentation. If, however, the observation was between the moon’s far limb and a star, subtract the moon’s semidiameter plus augmentation.
Clearing the Lunar
The information needed to continue with the calculations depended upon what method one used to clear the lunar (that is, to find the true distance). All methods, however, required the apparent lunar distance (result of Step 14), the sun or star’s apparent altitude (result of Step 8 or Step 11) and the moon’s apparent altitude (result of Step 11). All involved using the logarithms of trigonometric functions to find sine, cosine, tangent, secant, cosine, cotangent, most of which required making interpolations for each angle or distance used. The answer derived from Clearing the Lunar was the true distance between the moon and the other object per that observation.
Finding Longitude
We’re not done yet! After the true lunar distance has been calculated it is necessary to determine the Greenwich Apparent Time when that distance would have occurred. The Nautical Almanac gave the calculated distance between the moon and either the sun or one or more navigational stars for every three hours of the day. Using the sun-moon observation of 23 February 1805, for example, the cleared Lunar Distance was 66°32’16”. The Nautical Almanac shows that the true sun-moon distance was 66°43’36” at III hours (3 pm or 1500 hours) and 65°22’04” at VI hours (6 pm or 1800 hours). By proportion we can calculate that the Greenwich Apparent Time would have been 3hr 25m 01.4s pm (15:25:01.4 hours) when the true sun-moon distance was 66°32’16”. Then, as the true Local Apparent Time of the observation was 8:38:07.0 hours, the time difference would be 6 hours 46 minutes 54.4 seconds. Multiplying this by 15 gives a longitude of 101°43′ 36″ west, which should be rounded to 101°44′ west or more reasonably, 101¾°owing to in the uncertainties introduced by methodology, the numerous calculations and the observation itself. Even as late as 1900, the Nautical Almanac implied that the maximum accuracy obtainable from a lunar distance observation was plus or minus 5 minutes of longitude. Until the mid-1800s, an error of 15 minutes longitude from a lunar distance observation was considered tolerable. It was also for this reason that it was recommended to take as many observations as possible at a given location and use the average.
| Date | Observation type | Longitude | |
|---|---|---|---|
| 7 January 1805 | lunar distance | 100˚42′ west | |
| 15 January 1805 | eclipse | 101˚30′ west | 99˚24’45" (Lewis’s average) |
| 6 February 1805 | lunar distance | 100˚51′ west | |
| 23 February 1805 | lunar distance | 101˚44′ west | |
| 3 April 1805 | lunar distance | 100˚13′ west | |
| average longitude from Lewis’s observations | 101˚00′ west | ||
| redetermined longitude (map evaluation) | 101˚16’44" W |
Magnetic Declination
Lewis and Clark’s river and route surveys all were made using a magnetic compass. The bearings they recorded all were referenced to magnetic north. The Expedition’s surveys, thus had to be corrected to True North between the places where they obtained coordinates for latitude and longitude. The survey correcting, however, could have been done without taking observations for magnetic declination simply by plotting the survey between two points of known latitude and longitude. The true bearing and distance between those two points compared with the resultant bearing and distance between those two points would tell what scale factor to apply to the survey and how much rotation was needed to make it fit the true coordinates Perhaps it was easier just to take the observations for magnetic declination, calculate the declination and apply that correction to the surveyed bearings. Even this, however, would not tell how much to expand or shrink the estimated distances to make them fit.
Lewis took three observations at Fort Mandan to determine the magnetic declination. At some convenient time after the sun’s altitude usually was at least 10° above the horizon (to minimize the effects of refraction) Lewis would set out the artificial horizon. Meanwhile, Clark would set up the 6-inch diameter surveying compass (circumferentor) attaching it to a staff or stick firmly implanted in the ground. Using a spirit level (call it a miniature carpenter’s level) he would adjust the surveying compass so that it was level no matter what horizontal angle he measured. One of the men would be standing by with the chronometer to note the time. While Clark “tracked” the center of the sun through the slotted uprights of the surveying compass, Lewis took the sun’s altitude. As he did so he would signal to Clark to read the compass needle and the man at the chronometer to record the time. When this sequence of operations had been repeated two more times the observation was complete.
Lewis never made any calculations for magnetic declination. He could have done so using the steps outlined in Patterson’s Astronomy Notebook, either 1) calculating these three observations separately and then averaging the results or 2) he could have averaged the times, the bearings and the altitudes, then calculated the result. The latter operation is more expeditious, but the former sometimes shows where observational errors have been made.
| Date | Declination | Source |
|---|---|---|
| 1797? | 11½˚ east | Evans map |
| 25 March 1805 | 14½˚ east | Lewis and Clark, observed sun’s bearing, altitude and time |
| 1905 | 15½˚ east | Coast and Geodetic Survey |
| 1955 | 12˚ east | Coast and Geodetic Survey |
| 1990 | 10½˚ east | Coast and Geodetic Survey |
| 2005 | 9˚ east | Coast and Geodetic Survey |
Fort Mandan is a High Potential Historic Site along the Lewis and Clark National Historic Trail managed by the U.S. National Park Service. The North Dakota Department of Parks and Recreation manages a modern reconstruction and the Lewis and Clark Interpretive Center located at US Hwy 83 and ND Hwy 200A.
Knife River Indian Villages National Historic Site is a High Potential Historic Site along the Lewis and Clark National Historic Trail managed by the U.S. National Park Service. A unit of the National Park System, the site is located at 564 County Road 37, one-half mile north of Stanton, North Dakota. It has exhibits, trails, and a visitor center.
Notes
| ↑1 | Maps numbers are those given in Moulton, Journals, Vol. 1. |
|---|---|
| ↑2 | The meridian identified passes through the Mandan village. |
| ↑3 | St. Louis is at about 90°10′ west, thus the Evans map would place the Mandan village at about 107°43′ W. |
| ↑4 | This line is shown several miles south of the Mandan village. |
| ↑5 | That is, 11¼° East. |
| ↑6 | From Thompson’s celestial observations. |
| ↑7 | These coordinates for the Mandan village are approximate and likely are from David Thompson’s celestial observations. |
| ↑8 | The coordinates of this encampment were determined by “best-fit”-matching the Expedition’s latitudes and river survey to a detailed map by G.K. Warren (1856), a map by the Missouri River Commission (1895), “modern” maps and aerial photographs and descriptions of the site by early travelers. |
| ↑9 | The main reason the longitude Lewis derived was so far east of the actual longitude is that he made his time comparisons with those given in the Nautical Almanac using his calculated Local Mean Times. The times in the Nautical Almanac were given in Greenwich Apparent Time. For the later elements of the eclipse there was a difference of 9m47s between Mean Time and Apparent Time; that is, it was necessary to subtract 9m47s from Mean Time to convert it to Apparent Time (or add 9m47s to Apparent Time to obtain Mean Time). At 4 minutes per degree of longitude, this time difference of 9m47s moves Lewis’s calculated average longitude 2°27′ farther west to 101°51’45” West. |
| ↑10 | Lewis also made a mistake in how he determined his chronometer’s error. He might have discovered this if he had recalculated the times of his observations and made a plot (graph) of the chronometer’s rate of loss. From this plot he could have obtained more nearly correct times for the elements of the eclipse. These corrected times, however, move his longitudes about 20′ farther east. Subtracting this error of 20′ from 101°52′ gives an average longitude of 101°32′ west for Fort Mandan or about 15′ west of its actual location. |
| ↑11 | This should be 66°23’45” as sextant can be read only to the nearest 1/8 minute (7½ seconds). |
| ↑12 | This should be 66°21’22.5″ as sextant can be read only to the nearest 1/8 minute (7½ seconds). |
| ↑13 | This angular distance includes the sextant’s index error of 8’45”, which must be subtracted. Additionally, the sun’s semidiameter and moon’s semidiameter plus its augmentation need to be added to it. |
| ↑14 | To obtain this time, Lewis would be using a longitude of 99°24’55.5″ west though probably it was 99°25′, a rounded average of the two values he obtained from his observation of the eclipse. |
| ↑15 | At 15h15m57.7s Greenwich Apparent time the sun’s declination should have been -9°49’15.9″. The sun’s declination was 9°52’10” south at Greenwich Apparent Noon the 23rd and 9°30’06” south at Greenwich noon the 24th. |
| ↑16 | Hour angle (or HA) = sun’s hour angle. The sun’s forenoon Hour Angle = [(12h—Apparent AM Time of observation) x 15]. Lewis, however, should have calculated 50°25’30” [(12—8h38m18s) x 15 = 3h21m42.0s x 15 = 50°25’30.0″]. |
| ↑17 | The fault for the difference between the sun’s altitude that Lewis derived from Ellicott’s formula and Patterson’s lies in Robert Patterson‘s Astronomy Notebook that Lewis carried with him. In Patterson’s Problem 4th (“to compute the altitude of the sun, moon or any known star”), Example 1st, Form IV (A), step E, the instructions are to take the cosec (cosecant) of the sum of the Hour Angle and the Declination. Step E, however, should read cos (cosine). Using the cosine here produces an altitude of 17°24’19” for the sun’s center; essentially the same as that obtained by Ellicott’s formula. After obtaining these differences for the sun’s altitude, Lewis stopped, uncertain which value to use. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.




