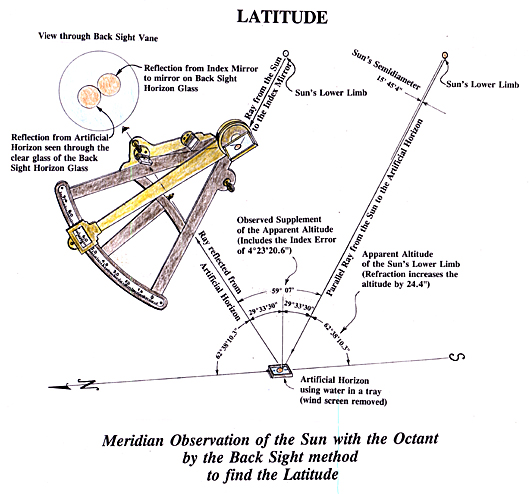
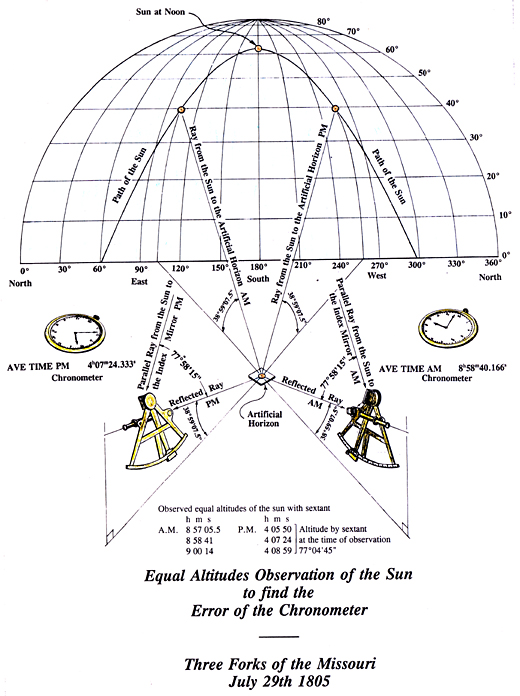
After Lewis had completed his Clearwater Canoe Camp observations, the celestial data would need to interpreted to determine their location.
Observations in Transit
After concealing their canoes in a pond near Fortunate Camp on the east side of the Continental Divide, the expedition traveled more than 330 miles overland to the Clearwater Canoe Camp. Clark’s survey between the two points (not including his exploration of the Salmon River) totals 400 miles. In all this distance the captains recorded taking celestial observations at just three places.
The first place was at the second or “upper” Lemhi Shoshone camp on 29 August 1804. On that date Clark recorded that they took observations, but gave no latitude, longitude, or observational data.
The second place was in the northern part of the Bitterroot Valley, along the Indian road, about eight miles south of Travelers’ Rest; the date was 9 September 1805. Rain and cloudy weather had prevailed since the expedition took leave of the Salish on 6 September 1805, but on the ninth the sky had cleared. Lewis, probably learning from Toby that they were about to start heading west over Lolo Trail, took advantage of the opportunity to make a meridian (noon) observation of the sun. Clark, on his map of their route (Atlas Map 68) misplaced this point of observation, locating it at the expedition’s camp for 4 September 1805 and 5 September 1805.
The third place that the captains took celestial observations was at Travelers’ Rest. During the evening of 9 September the sky remained clear, the moon was just past full; it was a ready-made occasion for Lewis to make a Lunar Distance observation. This he did, but after that observation he realized that the moon’s western limb already was imperfect and noted that the observation could not be depended on. The moon’s western limb, indeed, was imperfect, but (unknown to Lewis) the point on the moon’s limb to which he brought the star’s image into contact was still whole, and the observation could have provided valuable data if the captains had taken an Equal Altitudes on the 10th to determine the chronometer‘s error.
Strangely, although the weather was again fair, the captains took no Lunar Distance observation on the 10th, either. Lewis did take a meridian observation of the sun, but recorded no altitude observed nor did he or Clark record taking an Equal Altitudes observation. A possible explanation might be that Lewis needed to use the sextant to make the noon observation because one of the octant’s limbs already had been broken[1]“By several trials made today in order to adjust my Octant and ascertain her error in the direct observation, I found that it was 2° 1′ 45″ + or additive beyond the fracture; this … Continue reading (see Lewis, 16 February 1806), and he did not trust using the octant until he had checked its error.[2]Lewis, when taking an Equal Altitudes observation, always clamped the sextant’s index arm at the angle he had measured during the AM observation. To ensure that the angle he measured in the … Continue reading
Arrival
Eleven days of starving, freezing and struggling over the Lolo Trail had worn the Lewis and Clark Expedition to exhaustion. Though well met and given food by the Nez Perce at Weippe Prairie, the food so generously given did not agree with the travelers and many of them became sick. Barely able to travel, they continued a few days west from Weippe Prairie and arrived at the junction of two rivers. Here the captains made a camp and set the men to fell trees. From these they began to form their canoes, a task made easier when the Nez Perce showed them how to “burn out” the logs.
The captains clearly understood the need to obtain the latitude and longitude of this key place where travelers, once again, could take to river travel. As soon as they were well enough to make celestial observations, they did so. During their sojourn at this camp they made: 1) three sets of Equal Altitudes observation to determine the chronometer’s error at noon and its rate of loss; 2) two meridian altitude observations of the sun for latitude; 3) two observations for magnetic declination (variation of the compass); and 4) four observations of lunar distance for longitude.
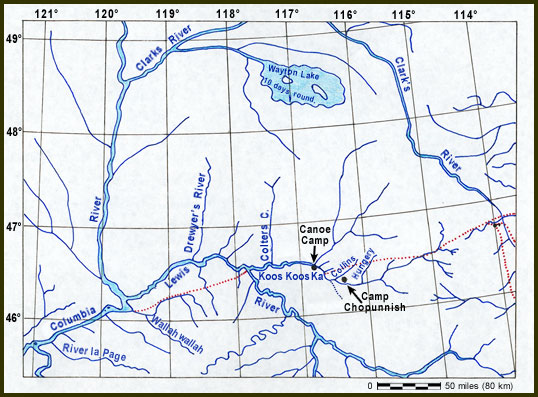
No archaeological evidence has yet surfaced to identify the exact site of Clearwater Canoe Campsite, and the junction of the Clearwater River and North Fork Clearwater River certainly has changed some since 1805. Nevertheless, the coordinates of that camp would have been near 46°30’05” North latitude, 116°19’46” West longitude (Lewis and Clark’s map of 1806—Atlas Map 123—shows this junction at about 46°43’N, 116°40’W); the river bank there is at about 900 feet above sea level.
Latitude
Canoe Camp and Long Camp[3]At their camp near Potlatch River (“Colters Creek”) on 6 May 1806, Lewis and Clark met three men of the “Skees-so-mish” people (Skitswish, later Coeur d’Alene), who … Continue reading
Determining the latitude of a location from a meridian observation of the sun is among the simplest celestial observations to take and to calculate. It is somewhat surprising, therefore, that Clark doesn’t mention taking an observation for the latitude at that camp until 5 October, and when he does, he writes: “Latitude of this place from the mean of two observations is 46°34’56.3″ North.” That’s it. No mention of the sun’s altitude they observed nor the date they took the observations, though it might be supposed that the last observation was taken on the 5th. The average latitude the captains obtained lies about 4’55” (5½ miles) north from the south side of the current river junction.
It is almost certain that the captains used the sextant to take the two meridian observations while at Clearwater Canoe Camp. Although the captains did not give the sun’s altitude for these two observations nor did they show their calculations, they had, since the mouth of the Ohio, recorded several observations they made with the sextant. For these observations they gave both the observed altitude[4]Observed altitude: This is the angle in degrees above the horizon that an observer instrumentally measures for a celestial body. With the sextant the captains usually measured the sun’s upper … Continue reading and their calculated latitude.[5]Calculated latitude: the observed altitude is but a starting place to determine the latitude. Many “corrections” are needed before the observed altitude is turned into a latitude. Usually … Continue reading Furthermore, while at Camp Dubois, Clark left many examples of his methodology and gave his calculated latitude.
As it is likely that the captains used the essentially the same methodology throughout the course of the expedition, it is possible to approximate what they might have observed at Clearwater Canoe Camp, even if it is just from the average.
The captains persistently made a mistake in calculating a latitude from an observation with the sextant while using the artificial horizon. This mistake was that they first divided the observed double altitude by two, then subtracted the full index error of the sextant (+8’45”), making all their calculated latitudes too high by 4’22½”. By correcting just that one error, the average latitude of Clearwater Canoe Camp recalculated from the average of their observations turns out to be 46°30’34” N–a difference of just 29″ too far north (about½ mile), not 4’55” too far north.
Possible Errors
The captains likely made other lesser mistakes in their calculating methodology, so it is not enough just to subtract 4’22½” from their latitude and have the latitude they should have obtained from the observation. Without the altitudes they observed, however, one can only suppose their observations might have provided latitudes that were somewhat more accurate than what their calculated latitudes appear to show.

Comment 1. In the calculation shown in the left-hand column, the double altitude of the sun’s upper limb is what the captains should have observed to fit the index error, refraction, semi-diameter, parallax, and declination given in the following steps.
Double Altitude: When taking a meridian altitude of the sun with a sextant or octant and using an artificial horizon, a ray from the sun that has been reflected from the index mirror to the horizon mirror and to the eye is matched with a ray that has been reflected from the artificial horizon through the horizon glass into the eye. This procedure gives the observer a true horizon on land, but doubles the true altitude of the object observed. This angle, therefore, must be divided by two to give the true observed altitude.
Comment 2. The calculation in the column on the right shows how the captains might have arrived at a latitude of 46°34’56” from the same “observed” double altitude. Using their method of calculating the latitude, and to fit the index error, refraction, semi-diameter, parallax and declination, this would be the average of the two double altitudes actually observed.
Comment 3. In the third step in both calculations, note the phrase “refraction at 990 feet.” Refraction is affected mainly by the density of the air above the observer. As one’s altitude increases the air becomes less dense; thus refraction typically decreases with altitude. But temperature also controls the density of the air, and that must be factored in.
A common formula for refraction is: ((983 x barometric pressure inches) / (460 + temperature in °F) x cotangent sun’s altitude). By this formula, at an altitude of 990 feet above sea level and a temperature of 60°F, the refraction would be 1’05”, whereas at sea level it would be 1’07.5″ For most observations using a sextant or octant it isn’t worth while to re-calculate refraction for every observation. The tabulated refraction at sea level found in the Tables Requisite is adequate. Besides, Lewis and Clark had no way of measuring their altitude above sea level at any point, and would necessarily have used the Tables Requisite, which they carried in their portable library. But for me, every second counts.
Alternate Methods
Although the captains did not provide the sun’s altitude for the meridian observations they took, they did record data from seven other observations from which the latitude of Clearwater Canoe Camp can be calculated. The data to calculate these latitudes come from the three Equal Altitudes observations (one each, morning and afternoon) and one observation for magnetic declination of the compass (variation of the needle). Unlike a Meridian Altitude observation of the sun–for which the observer does not need a chronometer or precise timepiece–to make a calculation for latitude from the sun’s altitude, declination and hour angle, it is necessary to have the correct Local Apparent Time.[6]Local Apparent Time: This is the time that is shown by the sun (sun dial time) at the place where you are. It is not the time shown at a standard meridian such as Mountain Standard Time (unless you … Continue reading This correct time generally comes from two Equal Altitudes observations taken a day apart, which give the chronometer’s error at local apparent noon on each day and, from that, the chronometer’s daily rate of loss or gain. Another element that is needed in these calculations is that the sun’s declination for the time of the observation must be determined from the Greenwich Time of the observation. This requires making an estimate of one’s longitude. Additionally, the sun’s altitude must be for its true center, and this requires making corrections to the observed altitude for index error, refraction, parallax and, usually, the sun’s semi-diameter.
Because the latitude calculated from the forenoon and afternoon Equal Altitudes observations on a given day usually were nearly the same, they were averaged for that day in the following table. The latitudes are rounded to the nearest second.

| 30 September | 46° 28′ 40″ | Equal Altitudes |
| 3 October | 46° 31′ 05″ | Equal Altitudes |
| 6 October | 46° 30′ 38″ | First observation for Magnetic Declination |
| 6 October | 46° 31′ 05″ | Equal Altitudes |
| Average | 46° 30′ 26″ | Equal Altitudes |
In this table the latitude of 46° 30′ 26″ would place the camp at the base of the mountain on the north side of the river.

Local Time
There are no journal entries to show that the chronometer’s time had been checked since 20 August 1804. If it had not, it is understandable that the captains felt it imperative to discover the chronometer’s error and rate of loss or gain. The reason for this is that the most critical element for determining the longitude is time. An Equal Altitudes observation, properly taken and corrected for the change in the sun’s declination, can reveal a chronometer’s error at Local Noon to within a second. It didn’t matter if the chronometer stopped or ran erratically most of the time provided it ran uniformly between two Equal Altitudes observations a day or, perhaps, two apart during which a Lunar Distance observation was made.
Chronometer Error on Local Apparent and Mean Time
The captains made Equal Altitudes observations on 30 September 1805, 3 October 1805, and 6 October 1805. For noon of the given date the chronometer was too fast on Local Time as follows:
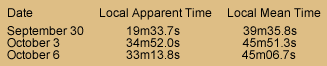
It would appear that the chronometer stopped sometime after the Equal Altitudes observation on 30 September, but started running again before the observation on 3 October. This conclusion is based on the tendency of the captains’ chronometer to lose time–never gain time–so how could it be 6m 15.5s faster on Local Mean Time on 3 October than it was on 30 September.
Chronometer’s Rate of Going
The chronometer lost 44.6 seconds on Mean Time between 3 October and 6 October. This rate of loss of about 15 seconds per day is essentially the same as what Lewis recorded for 22 July 1804 when he described his navigational instruments. The uncertainty about the chronometer’s error on Local Time for 30 September and its rate of loss between 30 September and 3 October produces some uncertainty about any longitude calculated from that day’s Lunar observations, but there are ways around this problem.
Example of a calculation from Equal Altitudes observation with the sextant to determine the chronometer’s error, 3 October:
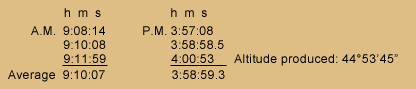
The time of 4:00:53 is from Moulton, 5:244. Thwaites has 4:00:05, but this is not possible.

Magnetic Declination
On 6 October the captains made two observations of the sun for magnetic declination (also called variation of the compass). The equipment used were the circumferentor (surveying compass), sextant, artificial horizon, spirit level and chronometer. These observations usually were taken early in the morning or late in the afternoon when the sun was low and could more easily be sighted in with the sight vanes of the surveying compass. The sun, however, had to be high enough so that refraction did not produce exaggerated readings for the sextant.
Lewis places the artificial horizon in a convenient position. He takes the sextant from its case and takes some preliminary sightings. Meanwhile, one of the men firmly sets or drives a staff or straight, sturdy branch into the ground in a near-vertical position. Clark takes the surveying compass from its box and places the ball joint on its underside over the stick or staff and secures it with a clamping screw. Next he takes the spirit level and sets it on the upper glass plate of the surveying compass. He loosens the ball-and-socket joint just enough so that he can accurately level the compass. When Clark is sure that the surveying compass is level, he loosens the clamping screw and rotates the compass toward the sun, aligning its sight vanes as near as he can with the sun’s center. The chronometer also has been taken out of its case and one of the men stands ready to record the time, sun’s bearing, and its altitude. Lewis now is ready and, adjusting the sextant’s index arm, matches the sun’s reflection from the artificial horizon with the sun’s reflection from the sextant’s index mirror to the mirror on the horizon glass and into his eye. Clark, all the while, has been “tracking” the sun. When Lewis has an exact match of images, he calls “Now!” The man at the chronometer reads the time at that instant, Clark reads the magnetic bearing shown by the compass needle, and Lewis reads the sun’s altitude from the sextant. When this process has been repeated one or more times, the observation is complete.
For the first magnetic observation taken at Clearwater Canoe Camp, Lewis “shot” the sun’s upper limb. He did this simply to reduce the effect of refraction. The second observation for Magnetic Declination was part of the Equal Altitude observation that followed the first observation for Magnetic Declination. At this time Lewis “shot” the sun’s center.

The declinations derived should have been closer to each other, but the surveying compass could not be read to closer than ± 1/2°, and an average of 18-1/2° East would be close enough for any hand-held compass.
Longitude
While at Clearwater Canoe Camp, the captains took four separate observations of Lunar Distance for longitude, one with the sun and three with stars. Only at their principal camps did the captains ever take that many observations for longitude. It’s not surprising, though, for they had traveled several hundred miles without an observation for longitude. Not only that, this junction is where a west-bound traveler could resume travel by water, and where an east-bound traveler would begin the difficult overland trip. It was essential that they determine the longitude of this camp.
30 September 1806
Less than 15 minutes after taking the afternoon set of Equal Altitude observations, the captains began taking observations of the angular distance between the west edge of the moon, then just past first Quarter, and the east edge of the sun. A simple average of the times gives 4h 28m 55s PM; the average of the distances (after correcting for an obvious error of 10 arc minutes on the 10th observation is 91°59’23”.
Although the chronometer’s error at the time of the observation is not known owing to its uncertain rate of loss, the Equal Altitudes observation showed that it was 29m 33.7s slow on Local Apparent Time at noon. If one uses the same rate of loss that can be established from the Equal Altitude observations taken on 3 and 6 October, the chronometer was losing 15 seconds in 24 hours. If true, in the nearly 4 hours between noon and the Lunar Distance observation it would have lost an additional 2.5 seconds, making the Local Apparent Time of the mean of the observation 3:59:18 PM.
By taking 1) the chronometer error at noon on the 30th, 2) the calculated time of the PM Equal Altitudes observation, and by 3) projecting this trend to the time that the chronometer showed for the Lunar observation on the 30th, one derives a time of 3:59:24 PM. Averaging this with 3:59:18 gives 3:59:21. The equivalent Greenwich Apparent Time is 11:44:40 PM.
3 October 1805
The captains measured the angular distance between the west (far) edge of the moon and the star Hamal (∝Arietis).[7]The Greek symbol for the letter Alpha (∝) identifies Hamal as the brightest star in the constellation Aries (The Ram). There was a gap of more than nine minutes between the first two observations, so the first data set should not be included in the averages. A plot of the data sets shows that some of them diverge widely from the smooth line that should result from the observations. In addition, there is an error in the distance of 77°59’00” for the sixth data set; that distance probably should be 78°00’00”. Nevertheless, using 78°00’00” for the sixth data set, the average distance is 78°00’10.0″; the average time is 8:30:10 PM.
6 October 1805
On this date the captains made two Lunar Distance observations. The first was with the star Altair (∝Aquilae)[8]Altair—Arabic for “flying eagle”—stands out brightly in the constellation Aquila (The Eagle). and the other with a star they identified as Aldebaran (∝Tauri).[9]Aldebaran, meaning “follower,” dominates its constellation, Taurus—the Bull—near the bull’s left eye. It is in fact the 13th brightest star in our sky. For their first observation the average chronometer time of the 10 sets of observations was 8:36:55 PM and the average angular distance was 58° 58′ 09.0″. The first three and last two data sets, however, seem to follow another trend. Using the five most consistent data sets gives an average chronometer time of 8:38:37 and the average angular distance 58° 58′ 27″.
For the second Lunar Distance observation on the 6th (from eight data sets) the average chronometer time was 9:16:42.4 PM. The angular distances, however, contain several problems (probably transcribing errors) and at least one error in distance by 1 arc minute. The plot, however, reveals that the first two and last three data are consistent enough to provide a usable average time and distance of 9:17:09 PM and 65° 25′ 51″. The 1805 Nautical Almanac, however, shows that at the time of the observation, the moon and Aldebaran should have been about 75° apart, not 65°. Additionally, Aldebaran, at the time of the observation, would not yet have risen above the tops of the adjacent mountains. It seems that the captains misidentified the star they observed, rendering their observation unusable.
Summary
The captains never calculated the longitude, nor did Ferdinand Rudolph Hassler, to whom some of the Corps’ data was given after the expedition’s return. The longitude of Clearwater Canoe Camp, as determined from present geographic features, places it at 116°19’46” West. On the map that Clark created at Fort Clatsop in February 1806 and completed sometime after the expedition, the camp is located at about 116°40′ West, as is shown in this redrafting of the section of the 1806 map from Travelers’ Rest to River la Page (John Day River). (Moulton’s Atlas Map 123).
Clark’s original map was made at a scale of about 1:3,000,000 (1 inch = approximately 50 miles). His “hybrid” latitude-longitude reticule has been replaced with one based on the Equidistant Conic Projection, and the sites of Clearwater Canoe Camp and Long Camp have been added.
Apparent Lunar Distance
Step 1
Plot the observed data. The data sets have a “fair” scatter, but the scatter seems to be equally distributed on either side of an average line; the average angular distance is 78°00’10”.
Step 2
Take the average time of the observations and correct it for the chronometer’s error and rate of loss. Because the chronometer sometimes ran erratically, it is best to average this time with the time projected for the observation from the chronometer’s error and the calculated time of the PM Equal Altitudes observation. The Local Apparent Time of the Lunar observation averaged from the two methods is 7:55:28 PM. From the estimated or “dead-reckoned” longitude of the place of observation, determine the Greenwich Apparent Time of the observation = 3:40:47 AM 7 October.
Step 3
Because the captains did not take measurements of the altitude of the moon and the star at the time of the observation, these altitudes must be computed by formula. This is a lengthy process because it involves making several sets of calculations using data from the Nautical Almanac and adjusting them to the calculated time of the observation. Needed are the Right Ascension[10]Right Ascension: The Right Ascension of a celestial body is the angle expressed in hours-minutes-seconds between that body and a point in the sky where the sun will be or was at the moment it crossed … Continue reading and the sun for noon on 6–7 October, the Right Ascension and Declination of the moon for midnight 6–7 October and at noon on 7 October, and the Right Ascension and Declination of the star Hamal.
Step 4
For the time of the observation, determine the Right Ascension of the sun (12h 38m 25.2s) and the Right Ascension (21h 15m 18.5s) and Declination (–12°53’59.3″) of moon. The Right Ascension and Declination of the star (01h 56m 17.3d, and 22° 32′ 26″) remain nearly the same for many years. Subtract the Right Ascension of sun from that of the moon and Hamal to find their angular separation from the sun with respect to the Celestial Equator.[11]Celestial Equator: The celestial equator is essentially the plane of the earth’s equator projected to the celestial sphere, which, in turn, is the imaginary globe upon whose surface all … Continue reading
Step 5
The Local Apparent Time of the observation is the sun’s hour angle. The difference in degrees from the sun’s hour angle gives the hour angle for the moon and Hamal (– 10°21’18” and –80°36’00”, respectively). From the hour angle, declination and known latitude, the true altitude of the moon and Hamal at the time of observation are calculated. The parallax and refraction for those altitudes then are calculated. The parallax is subtracted from the true altitude and the refraction is added to it to produce the “observed” altitude of the moon and Hamal, 29°05’48” and 22°29’19”, respectively. This process is repeated for the star Hamal: 22°29’19”.
Step 6
From the observed angular distance 78° 00′ 10″ subtract the sextant’s index error (8′ 45″). Find the moon’s semi-diameter in the 1805 Nautical Almanac (15′ 03″) and subtract that, because the star was “brought” to the side of the moon opposite the star. Next subtract the moon’s augmentation (8″ from the Tables Requisite for the moon’s altitude) and the result is the apparent distance: 77° 36′ 14″.
Now, let the calculations begin.
3 October 1805 Calculations
Patterson’s Problem 5, 2nd Example[12]Thomas Jefferson asked Robert Patterson (1743-1824), professor of mathematics at the University of Pennsylvania, to help Lewis develop his skills in making celestial observations. Jefferson wrote to … Continue reading

The following procedure departs from Patterson’s method and uses linear regression to find the Greenwich Apparent Time for the True Distance:

Did the captains really make a first-rate observation here, or was it just luck that the longitude calculated from it comes so close to the actual of 116°19’46” West? The other Lunar Distances produced longitudes that were much too far east: that on 30 September with the sun produced a longitude of 115° 46′ West, and that on 6 October with Altair produced a longitude of 114°49′. For the second Lunar Distance observation on 6 October the captains identified their target star as Aldebaran, but it was some other star.
Notes
| ↑1 | “By several trials made today in order to adjust my Octant and ascertain her error in the direct observation, I found that it was 2° 1′ 45″ + or additive beyond the fracture; this error was ascertained by a comparison with my sextant the error of which had been previously ascertained. the error of Octant in the direct observation on the broken limb next to 0 or 55° 20′ inclusive is 2° additive only.” Lewis, 16 February 1806. |
|---|---|
| ↑2 | Lewis, when taking an Equal Altitudes observation, always clamped the sextant’s index arm at the angle he had measured during the AM observation. To ensure that the angle he measured in the afternoon was exactly that measured in the forenoon, he left the index arm clamped until he had completed the PM observation. Consequently, if he took an Equal Altitudes observation he could not use the sextant for a Meridian Observation of the sun. |
| ↑3 | At their camp near Potlatch River (“Colters Creek”) on 6 May 1806, Lewis and Clark met three men of the “Skees-so-mish” people (Skitswish, later Coeur d’Alene), who told them of “a large lake in the mountains” near which they lived. Neither the source nor the meaning of “Wayton” is known. |
| ↑4 | Observed altitude: This is the angle in degrees above the horizon that an observer instrumentally measures for a celestial body. With the sextant the captains usually measured the sun’s upper limb; with the octant, its lower limb. |
| ↑5 | Calculated latitude: the observed altitude is but a starting place to determine the latitude. Many “corrections” are needed before the observed altitude is turned into a latitude. Usually the observed altitude is corrected first for the instrument’s index error. When an artificial horizon is used the resultant angle must be divided by two. Next, the effect of refraction is subtracted and the effect of parallax is added. Then the semi-diameter of the sun or moon is added if the lower limb was observed, or subtracted if the upper limb was observed. The declination of the celestial body at the time of the observation must be determined and algebraically subtracted. When all the above have been done, the result has to be subtracted from 90°, which, finally, is the calculated latitude. (And this is one of the simpler mathematical operations involving celestial observations.) |
| ↑6 | Local Apparent Time: This is the time that is shown by the sun (sun dial time) at the place where you are. It is not the time shown at a standard meridian such as Mountain Standard Time (unless you happen to be at 105° west longitude). Nor is it the time shown by a clock, because clocks keep mean or average time, which can differ from Apparent Time by more than 16 minutes. |
| ↑7 | The Greek symbol for the letter Alpha (∝) identifies Hamal as the brightest star in the constellation Aries (The Ram). |
| ↑8 | Altair—Arabic for “flying eagle”—stands out brightly in the constellation Aquila (The Eagle). |
| ↑9 | Aldebaran, meaning “follower,” dominates its constellation, Taurus—the Bull—near the bull’s left eye. It is in fact the 13th brightest star in our sky. |
| ↑10 | Right Ascension: The Right Ascension of a celestial body is the angle expressed in hours-minutes-seconds between that body and a point in the sky where the sun will be or was at the moment it crossed the celestial equator during the spring equinox. this point is called both the first point of Aries and the vernal equinox; it has a Right Ascension of 0h 00m 00.0s. the Right Ascension of the sun, moon, planets and brighter stars are calculated years in advance and published in a book called a Nautical Almanac, a copy of which was in the expedition’s portable library. The difference in Right Ascension between two bodies is the difference in time that they cross the upper meridian ( line due south from a person in the northern hemisphere). This difference, multiplied by 15, gives the angular separation of the two bodies referenced to the celestial equator. The celestial equator is essentially the plane of the earth’s equator projected to the celestial sphere, which, in turn, is the imaginary globe upon whose surface all celestial bodies are imagined to be affixed. |
| ↑11 | Celestial Equator: The celestial equator is essentially the plane of the earth’s equator projected to the celestial sphere, which, in turn, is the imaginary globe upon whose surface all celestial bodies are imagined to be affixed. |
| ↑12 | Thomas Jefferson asked Robert Patterson (1743-1824), professor of mathematics at the University of Pennsylvania, to help Lewis develop his skills in making celestial observations. Jefferson wrote to Patterson on 2 May 1803: “He [Lewis] has been for some time qualifying himself for taking observations of longitude & latitude to fix the geographical points of the line he will pass over, but little means are possessed here [in Washington City] of doing that; and it is the particular part in which you could give him valuable instruction, & he will receive it thankfully & employ it usefully.” For the benefit of his pupil, Patterson wrote an instruction manual that is now known as the Astronomy Notebook. Donald Jackson, Letters of the Lewis and Clark Expedition with Related Documents, 1783-1854 (2 vols., Urbana: University of Illinois Press: 1978), 1:21, 28-31. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.